Next: 3.3 The Rotating Reference
Up: 3.2 Measuring the Internal
Previous: 3.2.4 Four-Counter Geometry and
The Fourier transform of the complex muon polarization
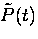 gives a good approximation of the actual internal
field distribution. The Fourier transform is
gives a good approximation of the actual internal
field distribution. The Fourier transform is
|  |
(29) |
Due to the finite counting rates, the Fourier transform contains
statistical noise.
The noisy or distorted portions of the asymmetry spectrum can be eliminated
from the Fourier transform through ``apodization''. Apodization is achieved
by multiplying the asymmetry spectrum by a weighting function
which varies between one and zero [48].
For example, the Fourier transform can be apodized with a Gaussian function
so that
| 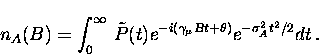 |
(30) |
Unfortunately, this apodization procedure also broadens the Fourier
transform. The apodization parameter 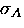 is chosen
to provide a compromise between the statistical noise in the spectrum
and the additional broadening of the spectrum which such a procedure introduces.
The Fourier transform will also appear broader than the actual
field distribution in the sample because the muon
spin precession signal is measured over a finite time interval.
Because of the finite number of recorded events, the integral in
Eq. (3.34) is replaced with a sum.
Examples of the Fourier transform of the muon precession signal in the
vortex state will be presented in the next chapter. Since
is chosen
to provide a compromise between the statistical noise in the spectrum
and the additional broadening of the spectrum which such a procedure introduces.
The Fourier transform will also appear broader than the actual
field distribution in the sample because the muon
spin precession signal is measured over a finite time interval.
Because of the finite number of recorded events, the integral in
Eq. (3.34) is replaced with a sum.
Examples of the Fourier transform of the muon precession signal in the
vortex state will be presented in the next chapter. Since
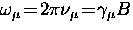 , the
Fourier transform can be presented as a function of either magnetic
field B or the muon precession frequency
, the
Fourier transform can be presented as a function of either magnetic
field B or the muon precession frequency 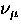 .
.




Next: 3.3 The Rotating Reference
Up: 3.2 Measuring the Internal
Previous: 3.2.4 Four-Counter Geometry and
![]() gives a good approximation of the actual internal
field distribution. The Fourier transform is
gives a good approximation of the actual internal
field distribution. The Fourier transform is