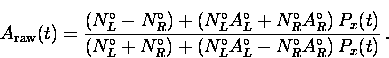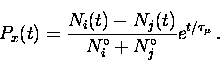Next: 3.2.2 The Corrected Asymmetry
Up: 3.2 Measuring the Internal
Previous: 3.2 Measuring the Internal
Consider a pair of opposing counters--e.g. L and R in
Fig. 3.1 with a magnetic field applied parallel to the
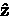 axis.
The ``raw asymmetry'' of the
histograms NL (t) and NR (t) is defined as
axis.
The ``raw asymmetry'' of the
histograms NL (t) and NR (t) is defined as
| ![\begin{displaymath}
A_{\rm raw} (t) \equiv A_{LR}(t) = \frac{ \left[ N_{L}(t)-B_...
...circ} \right]
+ \left[ N_{R}(t) - B_{R}^{\circ}
\right] } \, ,\end{displaymath}](img228.gif) |
(7) |
where
| ![\begin{displaymath}
N_{L}(t) = N_{L}^{\circ}e^{-t/ \tau_{\mu}} \left[ 1+A_{L}^{\...
...
\, P_{L}(t) \right] + B_{L}^{\circ} \,\,\, \hbox{\rm and},\\ \end{displaymath}](img229.gif) |
(8) |
| ![\begin{displaymath}
N_{R}(t) = N_{R}^{\circ}e^{-t/ \tau_{\mu}} \left[ 1+A_{R}^{\circ}
\, P_{R}(t) \right] + B_{R}^{\circ} \, ,\end{displaymath}](img230.gif) |
(9) |
so that
| ![\begin{displaymath}
A_{\rm raw}(t) = \frac{ N_{L}^{\circ} \left[ 1+A_{L}^{\circ}...
...]
+ N_{R}^{\circ} \left[ 1+A_{R}^{\circ} P_{R}(t) \right]} \, .\end{displaymath}](img231.gif) |
(10) |
The reason for introducing 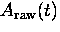 is to eliminate the
muon lifetime (which is a well known quantity)
and the random backgrounds
is to eliminate the
muon lifetime (which is a well known quantity)
and the random backgrounds 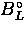 and
and 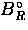 . Ideally,
the two counters in question are identical
to one another, so that the histograms recorded by the two counters differ
only by a phase. In this idealistic situation the
difference in phase between the histograms
is due solely to the geometry
of the positron counters with respect to the sample.
The polarization of the muon spin which is seen by
each counter is
. Ideally,
the two counters in question are identical
to one another, so that the histograms recorded by the two counters differ
only by a phase. In this idealistic situation the
difference in phase between the histograms
is due solely to the geometry
of the positron counters with respect to the sample.
The polarization of the muon spin which is seen by
each counter is
| 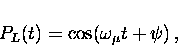 |
(11) |
| 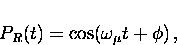 |
(12) |
where 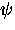 and
and 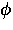 are the initial phases of the muon spin
polarization vector in counters L and R, respectively.
If the counters are aligned precisely opposite one another, the
difference between these phases is
are the initial phases of the muon spin
polarization vector in counters L and R, respectively.
If the counters are aligned precisely opposite one another, the
difference between these phases is
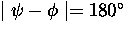 , so that
, so that
| ![\begin{displaymath}
P_{L}(t) = \cos[\omega_{\mu} + \, (\phi + \pi)]
= -\cos(\omega_{\mu} + \phi ) = -P_{R}(t) \, .\end{displaymath}](img239.gif) |
(13) |
The counters L and R measure the projection of the muon polarization
on the 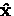 axis so that
axis so that
| 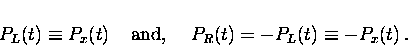 |
(14) |
Thus Eq. (3.7) becomes
| 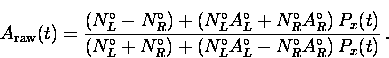 |
(15) |
If 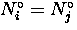 and
and 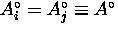 then Eq. (3.15) reduces to
then Eq. (3.15) reduces to
| 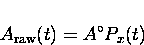 |
(16) |
If  ,
then using Eqs. (3.7), (3.8),
(3.9) and (3.16) the x-component of the
polarization can be written as
,
then using Eqs. (3.7), (3.8),
(3.9) and (3.16) the x-component of the
polarization can be written as
| 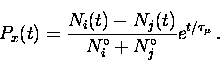 |
(17) |




Next: 3.2.2 The Corrected Asymmetry
Up: 3.2 Measuring the Internal
Previous: 3.2 Measuring the Internal
![]() axis.
The ``raw asymmetry'' of the
histograms NL (t) and NR (t) is defined as
axis.
The ``raw asymmetry'' of the
histograms NL (t) and NR (t) is defined as
![\begin{displaymath}
A_{\rm raw} (t) \equiv A_{LR}(t) = \frac{ \left[ N_{L}(t)-B_...
...circ} \right]
+ \left[ N_{R}(t) - B_{R}^{\circ}
\right] } \, ,\end{displaymath}](img228.gif)
![\begin{displaymath}
A_{\rm raw}(t) = \frac{ N_{L}^{\circ} \left[ 1+A_{L}^{\circ}...
...]
+ N_{R}^{\circ} \left[ 1+A_{R}^{\circ} P_{R}(t) \right]} \, .\end{displaymath}](img231.gif)
![]() is to eliminate the
muon lifetime (which is a well known quantity)
and the random backgrounds
is to eliminate the
muon lifetime (which is a well known quantity)
and the random backgrounds ![]() and
and ![]() . Ideally,
the two counters in question are identical
to one another, so that the histograms recorded by the two counters differ
only by a phase. In this idealistic situation the
difference in phase between the histograms
is due solely to the geometry
of the positron counters with respect to the sample.
The polarization of the muon spin which is seen by
each counter is
. Ideally,
the two counters in question are identical
to one another, so that the histograms recorded by the two counters differ
only by a phase. In this idealistic situation the
difference in phase between the histograms
is due solely to the geometry
of the positron counters with respect to the sample.
The polarization of the muon spin which is seen by
each counter is