The Raw Asymmetry For 2-Counter Geometry

Consider the pair of counters i and j in Fig. 3.11, analogous to counters R and L respectively in Fig. 3.10. In a real experiment one can define the raw asymmetry A_ij (t) of the appropriately paired histograms N_i (t) and N_j (t) defined by Eq. (3.16) as [77]:

$$A_{ij}(t) = \frac{ \left[ N_{i}(t)-B_{i}^{\circ} \right] - \ . . . . . . }^{\circ} \right] + \left[ N_{j}(t) - B_{j}^{\circ} \right] }$$ (17)

where

$$N_{i}(t) = N_{i}^{\circ}e^{-t/ \tau_{\mu}} \left[ 1+A_{i}^{\circ} \, P_{i}(t) \right] + B_{i}^{\circ}$$ (18)

$$N_{j}(t) = N_{j}^{\circ}e^{-t/ \tau_{\mu}} \left[ 1+A_{j}^{\circ} \, P_{j}(t) \right] + B_{j}^{\circ}$$ (19)

so that

$$A_{ij}(t) = \frac{ N_{i}^{\circ} \left[ 1+A_{i}^{\circ} P_{i} . . . . . . ight] + N_{j}^{\circ} \left[ 1+A_{j}^{\circ} P_{j}(t) \right]}$$ (20)

 

The motivation behind introducing A_ij (t) is the elimination of the muon lifetime (which is a well known quantity) and the random backgrounds $B_{i}^{\circ}$and $B_{j}^{\circ}$. In the ideal situation, the two counters in question are identical to one another so that the $\mu ^{+}$SR histograms recorded by each differ only by an initial phase. Because the muons travel for some time in the applied field before reaching the sample, their initial direction of polarization at the time of arrival in the sample is field dependent. However, the difference in phase between histograms is due solely to the geometry of the positron counters with respect to the sample. This situation is illustrated in Fig. 3.11. In the presence of a constant magnetic flux density B, the time evolution of the muon spin polarization vector $\vec{P} (t)$ is given in general by

$$P(t) = cos(2 \pi \nu_{\mu} + \theta)$$ (21)

where $\nu_{\mu} = \frac{\gamma_{\mu} B}{2 \pi}$ is the muon spin precession frequency and $\theta$ is the initial phase of the muon spin polarization vector. For counters i and j in Fig. 3.11, the polarization of the muon spin as seen by each counter is:

$$P_{i}(t) = \cos(2 \pi \nu_{\mu} + \psi)$$ (22)

$$P_{j}(t) = \cos(2 \pi \nu_{\mu} + \phi)$$ (23)

Since $\mid \psi - \phi \mid = 180^{\circ}$ then,

$$P_{i}(t) = \cos[2 \pi \nu_{\mu} + \, (\phi + \pi)] = -\cos(2 \pi \nu_{\mu} + \phi ) = -P_{j}(t)$$ (24)

With the counters i and j arranged symmetrically along the x and -x directions:

$$P_{i}(t) \equiv P_{x}(t) \; \; \; \; \hbox{\rm and}, \; \; \; \; P_{j}(t) = -P_{i}(t) \equiv -P_{x}(t)$$ (25)

Thus Eq. (3.17) becomes:

$$A_{ij}(t) = \frac{ \left( N_{i}^{\circ} - N_{j}^{\circ} \righ . . . . . . A_{i}^{\circ} - N_{j}^{\circ} A_{j}^{\circ} \right) P_{x}(t)}$$ (26)

If $N_{i}^{\circ} = N_{j}^{\circ}$ and $A_{i}^{\circ} = A_{j}^{\circ} \equiv A^{\circ}$ then Eq. (3.26) reduces to:

$$A_{ij}(t) = A^{\circ} P_{x}(t)$$ (27)

If $B_{i}^{\circ} = B_{j}^{\circ}$, then using Eqs. (3.17), (3.18), (3.19) and (3.27) the x-component of the polarization can be written as:

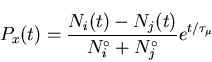$$P_{x}(t) = \frac{ N_{i}(t) - N_{j}(t) }{ N_{i}^{\circ} + N_{j}^{\circ}} e^{ t / \tau_{\mu}}$$ (28)