


Next: Calculation of the Core Radius
Up: Analysis
Previous: Model for the Internal Field Distribution
Fitting Software
The computer code for fitting the internal field model to the measured muon
spin polarisation
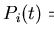 is written in FORTRAN.
The software incorporates Minuit function minimisation and error
analysis routines from the European Organisation for Nuclear
Research (CERN) program library. Using trial parameter values, the
fitting program calculates the distribution n(f) of muon precession
frequencies f according to the field model, and then from n(f) evaluates
the corresponding polarisation function (5.1). The code then
computes the chi-squared
is written in FORTRAN.
The software incorporates Minuit function minimisation and error
analysis routines from the European Organisation for Nuclear
Research (CERN) program library. Using trial parameter values, the
fitting program calculates the distribution n(f) of muon precession
frequencies f according to the field model, and then from n(f) evaluates
the corresponding polarisation function (5.1). The code then
computes the chi-squared  between this function and the
experimentally recorded muon spin polarisation
between this function and the
experimentally recorded muon spin polarisation
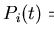 .
Minuit selects
new trial values for the variable parameters until it minimises
.
Minuit selects
new trial values for the variable parameters until it minimises 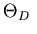 .
The
fitting program evolved from an earlier
version [49] to include the nonlocal corrections outlined
in the previous section and a square vortex lattice geometry.
.
The
fitting program evolved from an earlier
version [49] to include the nonlocal corrections outlined
in the previous section and a square vortex lattice geometry.
The fitting program determines the model distribution n(f) of
muon frequencies f by sampling the internal field B on a grid of evenly
spaced points within the vortex lattice primitive cell. Previous observations
(see Chapter 3) indicate that LuNi2B2C has a square vortex lattice
at the applied field
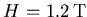 of the data analysed in this thesis.
Therefore the muon frequency distribution n(f) calculation employs the
vortex and reciprocal lattice vector geometry appropriate to a
square lattice under an applied field
H aligned with the
crystalline
c axis. In this case the vortex lattice primitive
axes
b1 and
b2 are
of the data analysed in this thesis.
Therefore the muon frequency distribution n(f) calculation employs the
vortex and reciprocal lattice vector geometry appropriate to a
square lattice under an applied field
H aligned with the
crystalline
c axis. In this case the vortex lattice primitive
axes
b1 and
b2 are
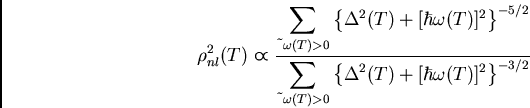
where the intervortex spacing
![$b = \sqrt{\smash[b]{\Phi_0/\overline{B}}}$](img181.gif) .
Figure 5.2 shows the sampled locations inside the vortex lattice
unit cell.
.
Figure 5.2 shows the sampled locations inside the vortex lattice
unit cell.
Figure 5.2:
Geometry for
ns2/2 = 32 sampling points within one eighth of the vortex
lattice unit cell. The dashed line and the
b1 axis bound the
sampled region.
The closed circles depict sampling points while the open ones
symbolise vortices. For data analyses
ns2/2 = 648.
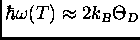 |
The square symmetry of the vortex lattice means the fitting software only
needs to sample one eighth of the unit cell. Then, when evaluating the
polarisation (5.1), the program weights
contributions from locations on the edge of the sampled area by a
compensatory factor of one half.
Similar symmetry considerations in reciprocal space greatly shorten the time
required to compute the field (5.2), and hence dramatically
speed up the fitting process. The analysis utilises a sampling density of
5184 points per vortex lattice primitive cell. This density is
sufficient since halving it only produces small changes (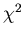 )
in the best-fit values of the penetration
depth
)
in the best-fit values of the penetration
depth 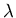 and the nonlocality parameter C, and in the calculated core
radius
and the nonlocality parameter C, and in the calculated core
radius 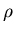 .
.
The ten fitted parameters are
- the average muon precession frequency of the superconducting
signal
 ,
,
- the penetration depth
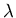 ,
,
- the nonlocality parameter C,
- the effective coherence length
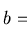 ,
,
- the initial amplitude of the asymmetry of the superconducting
signal A,
- the initial phase angle of the superconducting signal
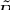 ,
,
- the effective depolarisation rate of the the superconducting
signal
 due to nuclear dipoles and vortex lattice disorder,
due to nuclear dipoles and vortex lattice disorder,
- the average muon precession frequency of the background signal fb,
- the initial phase angle of the background signal
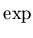 ,
and
,
and
- the effective depolarisation rate of the background signal
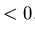 .
.
The data fitting proceeds by alternately letting only the superconducting and
then only the background signal parameters vary,
until all the variables converge to the final result.
Allowing the initial phases 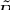 and
and  of the
superconducting and background signals to vary separately significantly
improves fit quality. During early fitting attempts the initial background
asymmetry Ab also varied and
grew unphysically large. Therefore throughout all subsequent fits
the initial background asymmetry Ab is fixed to 0.0044, as estimated
by comparing fast Fourier transforms (FFT) of the polarisation
signals measured in the superconducting and normal states.
In comparison, the asymmetry A of the superconducting signal is much
greater at
A = 0.237(2).
The fitting takes place within a rotating reference frame set to the
expected background signal frequency fb, facilitating easy visual inspection
of the accuracy of a fit. Knowledge of the best-fit values for the
internal field model parameters enables the extraction of the vortex
core radius
of the
superconducting and background signals to vary separately significantly
improves fit quality. During early fitting attempts the initial background
asymmetry Ab also varied and
grew unphysically large. Therefore throughout all subsequent fits
the initial background asymmetry Ab is fixed to 0.0044, as estimated
by comparing fast Fourier transforms (FFT) of the polarisation
signals measured in the superconducting and normal states.
In comparison, the asymmetry A of the superconducting signal is much
greater at
A = 0.237(2).
The fitting takes place within a rotating reference frame set to the
expected background signal frequency fb, facilitating easy visual inspection
of the accuracy of a fit. Knowledge of the best-fit values for the
internal field model parameters enables the extraction of the vortex
core radius 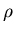 .
.



Next: Calculation of the Core Radius
Up: Analysis
Previous: Model for the Internal Field Distribution
Jess H. Brewer
2001-10-31
![]() is written in FORTRAN.
The software incorporates Minuit function minimisation and error
analysis routines from the European Organisation for Nuclear
Research (CERN) program library. Using trial parameter values, the
fitting program calculates the distribution n(f) of muon precession
frequencies f according to the field model, and then from n(f) evaluates
the corresponding polarisation function (5.1). The code then
computes the chi-squared
is written in FORTRAN.
The software incorporates Minuit function minimisation and error
analysis routines from the European Organisation for Nuclear
Research (CERN) program library. Using trial parameter values, the
fitting program calculates the distribution n(f) of muon precession
frequencies f according to the field model, and then from n(f) evaluates
the corresponding polarisation function (5.1). The code then
computes the chi-squared ![]() between this function and the
experimentally recorded muon spin polarisation
between this function and the
experimentally recorded muon spin polarisation
![]() .
Minuit selects
new trial values for the variable parameters until it minimises
.
Minuit selects
new trial values for the variable parameters until it minimises ![]() .
The
fitting program evolved from an earlier
version [49] to include the nonlocal corrections outlined
in the previous section and a square vortex lattice geometry.
.
The
fitting program evolved from an earlier
version [49] to include the nonlocal corrections outlined
in the previous section and a square vortex lattice geometry.
![]() of the data analysed in this thesis.
Therefore the muon frequency distribution n(f) calculation employs the
vortex and reciprocal lattice vector geometry appropriate to a
square lattice under an applied field
H aligned with the
crystalline
c axis. In this case the vortex lattice primitive
axes
b1 and
b2 are
of the data analysed in this thesis.
Therefore the muon frequency distribution n(f) calculation employs the
vortex and reciprocal lattice vector geometry appropriate to a
square lattice under an applied field
H aligned with the
crystalline
c axis. In this case the vortex lattice primitive
axes
b1 and
b2 are
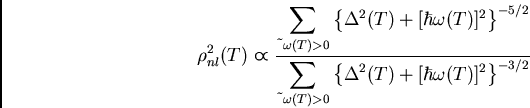
![]() .
Figure 5.2 shows the sampled locations inside the vortex lattice
unit cell.
.
Figure 5.2 shows the sampled locations inside the vortex lattice
unit cell.
 ,
,