


Next: A.2 Longitudinal Field Polarization
Up: A Muonium Spin Polarization
Previous: A Muonium Spin Polarization
Now that we have the eigenvectors and eigenvalues of all four
muonium states it is a straightforward task to calculate
the matrix elements of the muon spin operator.
Initially, the muon beam is virtually 100% spin polarized in any 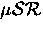 experiment using surface muons.
In the case of a transverse field experiment the initial
muon spin direction is perpendicular to the applied magnetic field,
conventionally along the
experiment using surface muons.
In the case of a transverse field experiment the initial
muon spin direction is perpendicular to the applied magnetic field,
conventionally along the 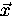 axis,
so we have an initial muon state given by
axis,
so we have an initial muon state given by
| 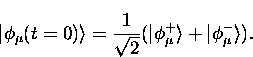 |
(13) |
Since electrons of the stopping medium (which are captured by muons
to form muonium) are unpolarized, we have two initial muonium
states possible - with the electron spin either up or
down.
It is has always been assumed that these are formed
with equal probability; no observable departure from this has
ever been reported,
so we have equal contributions from each of the initial states
Considering the first of these we can write, using Eq. (A.17),
At a later time t, when the initial state has evolved
under the Hamiltonian, we have
Expanding the Hamiltonian in terms of operators and
the wavefunctions in terms of the basis states, we have
giving
So we have, for that fraction of muonium formed with
electron spin ``up'', the contribution to
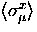 of
of
The other fraction, with an initial state in which the electron spin
is ``down",
| 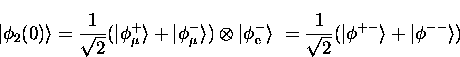 |
(14) |
is treated in a similar way, giving
| 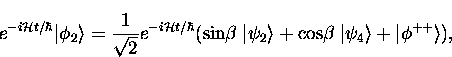 |
(15) |
and a contribution to the spin polarization of
| 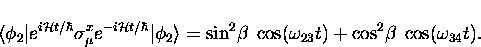 |
(16) |
The total polarization is simply the sum
| ![\begin{displaymath}
P_{\mu}^x(t) =\frac{1}{2} \left\{
\cos^2\!\beta \; \left[ ...
...ft[ \cos(\omega_{14}t)
+ \cos(\omega_{23}t) \right] \right\}.\end{displaymath}](img338.gif) |
(17) |
In weak magnetic fields of not more than about 8 G the difference
between 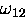 and
and 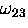 is small enough
that it can usually be ignored; the signal appears to have
only one component at the average muonium frequency
is small enough
that it can usually be ignored; the signal appears to have
only one component at the average muonium frequency 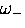 .In higher field the splitting that originates with the
hyperfine interaction term of the Hamiltonian is immediately
apparent in the polarization function as beating of the these
two components, the hyperfine frequency
.In higher field the splitting that originates with the
hyperfine interaction term of the Hamiltonian is immediately
apparent in the polarization function as beating of the these
two components, the hyperfine frequency 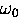 can be obtained
from the difference of the two frequencies
can be obtained
from the difference of the two frequencies
| ![\begin{displaymath}
\omega_{23} - \omega_{12} = \left[\omega_0^2 + 4\omega_+^2 \right]^{1/2}
- \omega_0.\end{displaymath}](img340.gif) |
(18) |
For unperturbed muonium (in vacuum, for example) the hyperfine
frequency is 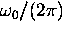 = 4463 Mhz. [4]
(In condensed matter nearby molecules can cause a distortion of the 1s
orbital of the muonium electron, changing the electron
spin density at the muon which is reflected in a shift
of the hyperfine frequency.)
= 4463 Mhz. [4]
(In condensed matter nearby molecules can cause a distortion of the 1s
orbital of the muonium electron, changing the electron
spin density at the muon which is reflected in a shift
of the hyperfine frequency.)
Since the high frequency transitions 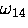 and
and 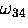 are not resolved
by the timing electronics of most
are not resolved
by the timing electronics of most 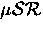 spectometers, those terms
average to zero, and in fields sufficiently weak that
the amplitudes of the remaining signals are approximately equal,
the polarization function reduces to
spectometers, those terms
average to zero, and in fields sufficiently weak that
the amplitudes of the remaining signals are approximately equal,
the polarization function reduces to
| ![\begin{displaymath}
P_{\mu}^x(t) \simeq \frac{1}{4} \left [\cos(\omega_{12} t) +
\cos(\omega_{23} t) \right ].\end{displaymath}](img344.gif) |
(19) |



Next: A.2 Longitudinal Field Polarization
Up: A Muonium Spin Polarization
Previous: A Muonium Spin Polarization
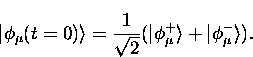
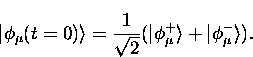
![]() of
of
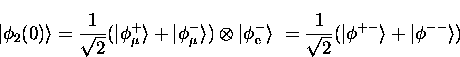
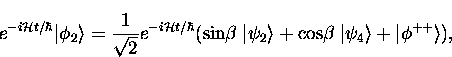
![\begin{displaymath}
P_{\mu}^x(t) =\frac{1}{2} \left\{
\cos^2\!\beta \; \left[ ...
...ft[ \cos(\omega_{14}t)
+ \cos(\omega_{23}t) \right] \right\}.\end{displaymath}](img338.gif)
![]() and
and ![]() is small enough
that it can usually be ignored; the signal appears to have
only one component at the average muonium frequency
is small enough
that it can usually be ignored; the signal appears to have
only one component at the average muonium frequency ![]() .In higher field the splitting that originates with the
hyperfine interaction term of the Hamiltonian is immediately
apparent in the polarization function as beating of the these
two components, the hyperfine frequency
.In higher field the splitting that originates with the
hyperfine interaction term of the Hamiltonian is immediately
apparent in the polarization function as beating of the these
two components, the hyperfine frequency ![]() can be obtained
from the difference of the two frequencies
can be obtained
from the difference of the two frequencies
![\begin{displaymath}
\omega_{23} - \omega_{12} = \left[\omega_0^2 + 4\omega_+^2 \right]^{1/2}
- \omega_0.\end{displaymath}](img340.gif)
![]() and
and ![]() are not resolved
by the timing electronics of most
are not resolved
by the timing electronics of most ![]() spectometers, those terms
average to zero, and in fields sufficiently weak that
the amplitudes of the remaining signals are approximately equal,
the polarization function reduces to
spectometers, those terms
average to zero, and in fields sufficiently weak that
the amplitudes of the remaining signals are approximately equal,
the polarization function reduces to
![\begin{displaymath}
P_{\mu}^x(t) \simeq \frac{1}{4} \left [\cos(\omega_{12} t) +
\cos(\omega_{23} t) \right ].\end{displaymath}](img344.gif)