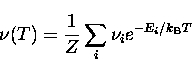
There also remains the possibility that the Mu tunnels rapidly from excited states, in which the barrier height and width would be reduced, so that the temperature dependence in the hop rate we measure is merely due to the temperature dependence of the probability of muonium occupying an excited state. We consider here a calculation of the vibrational frequency and the energy level separation of the harmonic oscillator modes of the muonium atom in the potential well defined by the xenon cage.
When several levels may be populated the total tunnelling rate from one potential well to another is the sum, assuming the states are populated according to the Boltzman distribution,
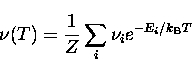 |
(28) |
The Xe-H pair potential, at close distances r where the interaction is strongly repulsive, is approximated using the Born-Mayer potential
| (29) |
The Lennard-Jones (6,12) potential for the Xe-H pair
![\begin{displaymath}
V_{\rm LJ} = \eta \left[ (r_0/r)^{12} - 2(r_0/r)^6 \right]\end{displaymath}](img294.gif) |
(30) |
Within about 1Å of the equilibrium position of the Mu atom in the Xe cage this potential is very well approximated by a harmonic oscillator potential
| (31) |
| (32) |
If the Xe atoms are allowed to move away
from the Mu atom, relaxing the strain imposed by the short
Xe-Mu distance, the larger space for the Mu atom lowers the
energy levels.
The size of this shift can be estimated by iteratively minimizing
the potential energy of Xe atoms and the Mu atom in a finite
cluster of atoms.
This calculation was done for a ![]() unit cell
cluster, with the Xe atoms at the surfaces of the cluster
held at fixed positions of the undisturbed Xe lattice, and a
Mu atom at the octahedral site of the central unit cell.
After allowing all of the interior Xe atoms to find their new
local potential minima, the new sites of the 6 nearest-neighbour
Xe atoms that define the
octahedral site are found to be displaced 0.20 Å away from the Mu atom.
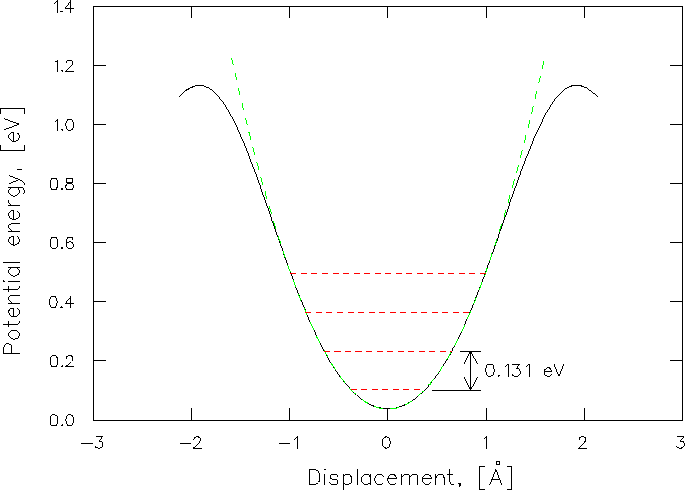
The potential of the Mu atom was then computed along the (111) direction
through the octahedral site, with the lattice atoms now fixed,
as shown in Fig. 6.31. (The heavy Xe atoms
will not be able to follow the fast motion of the Mu atom.)
Near the octahedral site the Mu potential is
characterised by a force constant
d = 0.485 eV/Å2, and is indicated by the dashed line.
The first few energy levels of the resulting quantum harmonic oscillator
unit cell
cluster, with the Xe atoms at the surfaces of the cluster
held at fixed positions of the undisturbed Xe lattice, and a
Mu atom at the octahedral site of the central unit cell.
After allowing all of the interior Xe atoms to find their new
local potential minima, the new sites of the 6 nearest-neighbour
Xe atoms that define the
octahedral site are found to be displaced 0.20 Å away from the Mu atom.
The potential of the Mu atom was then computed along the (111) direction
through the octahedral site, with the lattice atoms now fixed,
as shown in Fig. 6.31. (The heavy Xe atoms
will not be able to follow the fast motion of the Mu atom.)
Near the octahedral site the Mu potential is
characterised by a force constant
d = 0.485 eV/Å2, and is indicated by the dashed line.
The first few energy levels of the resulting quantum harmonic oscillator
![]() are also shown, in which
are also shown, in which
![]() eV,
about 2.7 times larger than the measured activation energy Ea.
eV,
about 2.7 times larger than the measured activation energy Ea.
 |
We should conclude from this that classical thermal activation to excited states cannot be ruled out as being responsible for the temperature dependence of the Mu diffusion rate; the similarity of the calculated energy to the measured activation energy is simply too close for this question to be settled by this model. If muonium diffuses in solid Xe by quantum tunnelling, there is no evidence that barrier fluctuations play a role at any temperature, even under the most promising conditions for its detection.
At the temperatures being considered here there is a difficulty with any model involving coupling to phonons: the lack of knowledge of the frequency-dependence of the coupling parameters at frequencies that are no longer small compared to the Debye frequency. Further progress in understanding exactly how the interstitial couples to lattice excitations at frequencies where the solid is no longer Debye-like is clearly necessary if we are to fully understand the role of phonons in quantum diffusion. For example, direct measurement of the coupling constants as a function of wave vector (and polarization with respect to the lattice) are in principle possible by measuring the muonium hop rate while injecting phonons of a single wave vector at low temperture. This would have an enormous advantage over the indiscriminate thermal excitation of the entire phonon spectrum which has been the only method used thus far.