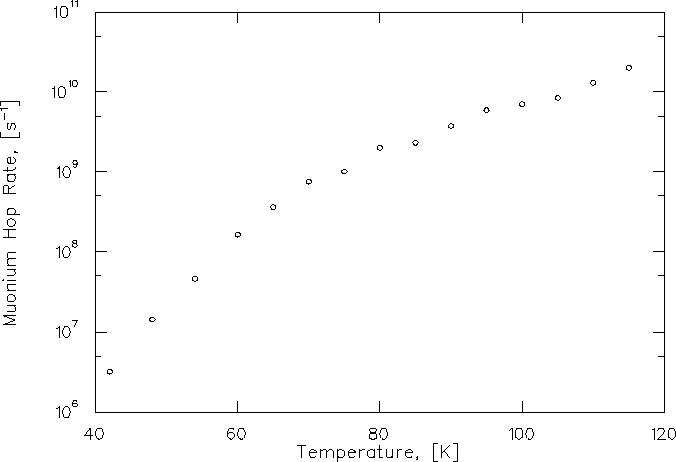


Next: 6.7 Numerical Evaluation of
Up: 6 Quantum Diffusion II:
Previous: 6.5 One-Phonon Quantum Diffusion
Muonium spin polarization spectra were measured in solid Xe by both
TF and LF methods.
The relaxation of the polarization in the LF case occurs as a result
of the motion of the Mu atom among atoms of the host lattice, some of
which are isotopes with nuclear moments.
The nuclear hyperfine (nhf) interaction between the electron bound in
the Mu atom and surrounding nuclear moments leads to an
additional term in the
Hamiltonian describing Mu spin dynamics:
| 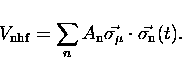 |
(24) |
This problem is made tractable by approximating this interaction
with an effective time-dependent magnetic field 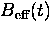 which fluctuates both in direction
and magnitude as a result of the motion of the Mu atom.
The Fourier transform of
which fluctuates both in direction
and magnitude as a result of the motion of the Mu atom.
The Fourier transform of 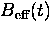 gives
the spectral function
gives
the spectral function 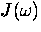 of the fluctuating effective field.
Transitions among the states of the Mu atom differing in energy
by
of the fluctuating effective field.
Transitions among the states of the Mu atom differing in energy
by 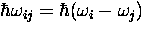 are induced
in proportion to
are induced
in proportion to 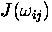 , hence changing the muon spin
state and irreversibly reducing the muon spin polarization.
The resulting muon spin polarization function
was calculated by Celio and Meier [63]
and Celio and Yen [64,65].
, hence changing the muon spin
state and irreversibly reducing the muon spin polarization.
The resulting muon spin polarization function
was calculated by Celio and Meier [63]
and Celio and Yen [64,65].
For slowly diffusing muonium where 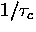 is small
compared to all transition frequencies except the
smallest -
is small
compared to all transition frequencies except the
smallest - 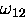 - the relaxation function is
well approximated by a simple exponential with a
relaxation rate
- the relaxation function is
well approximated by a simple exponential with a
relaxation rate
| 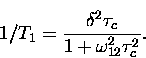 |
(25) |
The temperature dependence of this relaxation rate
is shown in Fig. 6.27, demonstrating that,
at least for temperatures from 40 to 120 K,
the muonium hop rate increases with temperature.
In general the time evolution of the muon polarization is a
complicated function of the inverse correlation time
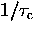 , the exchange coupling
, the exchange coupling 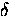 and LF
field B, which can be calculated numerically by the algorithm
due to Celio.
The muonium diffusion hop rate
and LF
field B, which can be calculated numerically by the algorithm
due to Celio.
The muonium diffusion hop rate 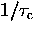 at each temperature
is extracted from the LF data by simultaneously fitting the polarization
functions measured in several different magnetic fields to the
complete theoretical polarization function.
The resultant temperature dependence of the Mu hop rate
is shown in Fig. 6.28.
at each temperature
is extracted from the LF data by simultaneously fitting the polarization
functions measured in several different magnetic fields to the
complete theoretical polarization function.
The resultant temperature dependence of the Mu hop rate
is shown in Fig. 6.28.
In order to elucidate the nature of the peculiar change
in relaxation rate at temperatures above T=130 K, a TF
experiment on a sample of solid 136Xe was also performed.
The resulting relaxation rate 1/T2 is
also shown in Fig. 6.27.
Since 136Xe atoms do not have nuclear moments
there should not be any contribution to spin relaxation
due to dipolar broadening.
Electric field  experiments were unable to cause any change
in the polarization function at any temperature, so we cannot be
certain exactly what caused the addition relaxation, however it
is probably of a chemical nature, and comes into effect at high
temperatures where the muonium is most rapidly diffusing.
We will therefore restrict ourselves to temperatures below 120 K
where this anomalous contribution to the relaxation rate
in longitudinal field is negligible.
experiments were unable to cause any change
in the polarization function at any temperature, so we cannot be
certain exactly what caused the addition relaxation, however it
is probably of a chemical nature, and comes into effect at high
temperatures where the muonium is most rapidly diffusing.
We will therefore restrict ourselves to temperatures below 120 K
where this anomalous contribution to the relaxation rate
in longitudinal field is negligible.
Figure 6.27:
Muonium spin relaxation rates in solid Xe.
Longitudinal relaxation rates 1/T1 measured in natural solid Xe
in various magnetic fields (triangles:1451 G, circles:725 G, squares:363 G,
stars: 72 G and crosses:21 G).
The other points (diamonds) are 1/T2 measured in solid 136Xe.
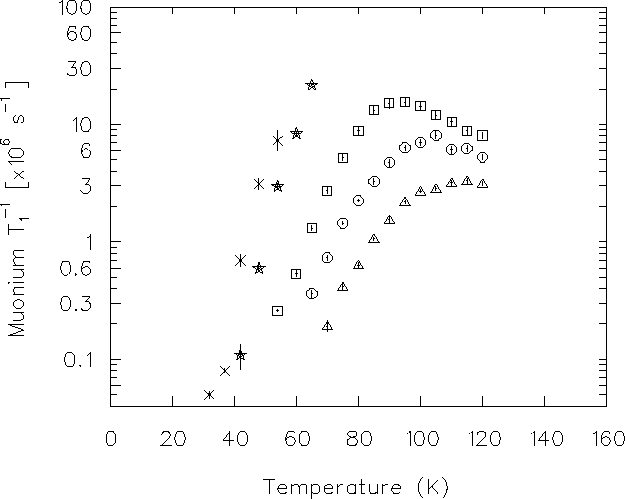 |
Figure 6.28:
Muonium hop rate in solid Xe extracted from the LF
data by simultaneous fits to data in different magnetic fields
at each temperature.
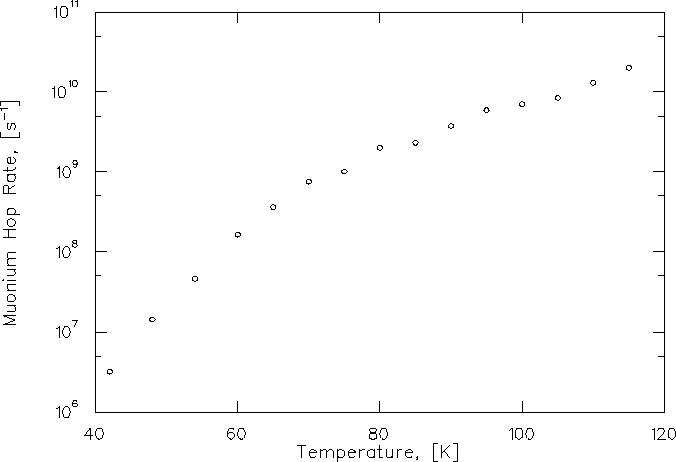 |
The same results are also presented in the form of an Arrhenius plot
in Fig. 6.30.
The hop rate as a function of temperature can be fitted
quite adequately to an Arrhenius function,
| 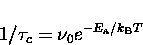 |
(26) |
representing a simple over-barrier classical hopping mechanism with
hop attempt rate 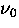 and activation energy
and activation energy 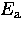 .Such a fit yields
.Such a fit yields
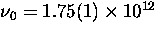 s-1, about twice
the Debye frequency, and a barrier height
s-1, about twice
the Debye frequency, and a barrier height 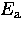 = 0.0482(2) eV.
It is difficult to immediately rule out this mechanism on
grounds of the barrier height, since it is not unreasonable.
(We shall, however, discuss a calculation of the shape of
the potential well of Mu in Xe in Section 6.8, which estimates
the depth of the potential well to be about 1 eV.)
On the other hand, the indicated attempt frequency is
more than a factor of 10 smaller than what one expects.
The attempt rate on the barrier in the case of over-barrier
activation would be the zero-point frequency
= 0.0482(2) eV.
It is difficult to immediately rule out this mechanism on
grounds of the barrier height, since it is not unreasonable.
(We shall, however, discuss a calculation of the shape of
the potential well of Mu in Xe in Section 6.8, which estimates
the depth of the potential well to be about 1 eV.)
On the other hand, the indicated attempt frequency is
more than a factor of 10 smaller than what one expects.
The attempt rate on the barrier in the case of over-barrier
activation would be the zero-point frequency 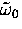 of the particle in the well.
Since the interaction between atoms of a van der Waals solid
has the same origin as the barrier to diffusion of muonium atoms
we can make a rough estimate of
of the particle in the well.
Since the interaction between atoms of a van der Waals solid
has the same origin as the barrier to diffusion of muonium atoms
we can make a rough estimate of 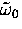 by assuming that the interstitial occupies a site
where it is subject to a potential similar
to that which holds the lattice atoms at their
equilibrium positions.
Assuming a harmonic potential, we may scale the Debye frequency
by the root of the ratio of the lattice atom's mass to
the interstitial's mass:
by assuming that the interstitial occupies a site
where it is subject to a potential similar
to that which holds the lattice atoms at their
equilibrium positions.
Assuming a harmonic potential, we may scale the Debye frequency
by the root of the ratio of the lattice atom's mass to
the interstitial's mass:
| 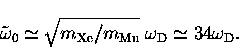 |
(27) |
Measurements of the vibrational frequencies of hydrogen
and deuterium embedded in solid Xe agree quite well
with this approximation.
[58,60]
Consequently, this result allows us to rule out
classical over-barrier hopping being responsible for the observed hop
rate since the expected frequency is about 17 times larger
than the Arrhenius plot indicates.



Next: 6.7 Numerical Evaluation of
Up: 6 Quantum Diffusion II:
Previous: 6.5 One-Phonon Quantum Diffusion
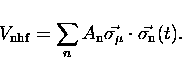
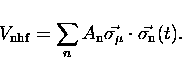
![]() is small
compared to all transition frequencies except the
smallest -
is small
compared to all transition frequencies except the
smallest - ![]() - the relaxation function is
well approximated by a simple exponential with a
relaxation rate
- the relaxation function is
well approximated by a simple exponential with a
relaxation rate
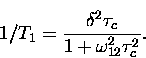
![]() , the exchange coupling
, the exchange coupling ![]() and LF
field B, which can be calculated numerically by the algorithm
due to Celio.
The muonium diffusion hop rate
and LF
field B, which can be calculated numerically by the algorithm
due to Celio.
The muonium diffusion hop rate ![]() at each temperature
is extracted from the LF data by simultaneously fitting the polarization
functions measured in several different magnetic fields to the
complete theoretical polarization function.
The resultant temperature dependence of the Mu hop rate
is shown in Fig. 6.28.
at each temperature
is extracted from the LF data by simultaneously fitting the polarization
functions measured in several different magnetic fields to the
complete theoretical polarization function.
The resultant temperature dependence of the Mu hop rate
is shown in Fig. 6.28.
![]() experiments were unable to cause any change
in the polarization function at any temperature, so we cannot be
certain exactly what caused the addition relaxation, however it
is probably of a chemical nature, and comes into effect at high
temperatures where the muonium is most rapidly diffusing.
We will therefore restrict ourselves to temperatures below 120 K
where this anomalous contribution to the relaxation rate
in longitudinal field is negligible.
experiments were unable to cause any change
in the polarization function at any temperature, so we cannot be
certain exactly what caused the addition relaxation, however it
is probably of a chemical nature, and comes into effect at high
temperatures where the muonium is most rapidly diffusing.
We will therefore restrict ourselves to temperatures below 120 K
where this anomalous contribution to the relaxation rate
in longitudinal field is negligible.