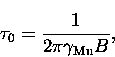Muonium formation involving electrons originating in the radiolysis track
depends on the transport of these electrons to the muon under
the influence of their mutual Coulomb attraction and any external
fields.
The associated time-of-flight can be large enough to
have an observable effect on timescales accessible by ![]() if the initial separation is great enough.
if the initial separation is great enough.
While a muon awaits the arrival of an electron
its spin will precess in an external transverse magnetic field
at the muon Larmor frequency ![]() , and if it decays
during this time it will contribute to the diamagnetic signal.
Those muons that do not decay while in a diamagnetic state
will, upon forming muonium, begin to precess
in the opposite sense at the characteristic frequencies
, and if it decays
during this time it will contribute to the diamagnetic signal.
Those muons that do not decay while in a diamagnetic state
will, upon forming muonium, begin to precess
in the opposite sense at the characteristic frequencies
![]() and
and ![]() , possibly contributing
to the muonium signal instead.
(A complete discussion of the muonium signal is given in
Appendix A.
In weak fields we may characterize the muonium signal by
the average frequency
, possibly contributing
to the muonium signal instead.
(A complete discussion of the muonium signal is given in
Appendix A.
In weak fields we may characterize the muonium signal by
the average frequency ![]() .)
The elapsed time between muons entering the sample
and the arrival of electrons at the muons will
have some distribution, so the coherent diamagnetic polarization
will be converted to muonium polarization
over a range of times, with a corresponding distribution
in the apparent initial phase of the muonium precession.
Since
.)
The elapsed time between muons entering the sample
and the arrival of electrons at the muons will
have some distribution, so the coherent diamagnetic polarization
will be converted to muonium polarization
over a range of times, with a corresponding distribution
in the apparent initial phase of the muonium precession.
Since ![]() is very small
compared to the muonium precession frequencies,
the dephasing is almost entirely
due to precession in the higher frequency final state
starting at different times.
The conversion of coherent muon polarization to partially
dephased muonium polarization results in a measureable
loss of asymmetry whenever the formation time is comparable
to or larger than the muonium precession period.
Delayed muonium formation is experimentally observable in principle
in the shape of the diamagnetic relaxation function
is very small
compared to the muonium precession frequencies,
the dephasing is almost entirely
due to precession in the higher frequency final state
starting at different times.
The conversion of coherent muon polarization to partially
dephased muonium polarization results in a measureable
loss of asymmetry whenever the formation time is comparable
to or larger than the muonium precession period.
Delayed muonium formation is experimentally observable in principle
in the shape of the diamagnetic relaxation function
![]() , but it is more easily observed
in the resulting muonium amplitude and phase after all Mu formation
is complete.
A stronger magnetic field results in proportionally
more dephasing and therefore a reduced polarization of the delayed
part of the muonium ensemble.
One can thus estimate the characteristic time of muonium formation
from the magnetic field dependence of the amplitude of the
muonium signal.
, but it is more easily observed
in the resulting muonium amplitude and phase after all Mu formation
is complete.
A stronger magnetic field results in proportionally
more dephasing and therefore a reduced polarization of the delayed
part of the muonium ensemble.
One can thus estimate the characteristic time of muonium formation
from the magnetic field dependence of the amplitude of the
muonium signal.
At any time the instantaneous polarization is the vector sum of all
muon spins present including diamagnetic, delayed and prompt muonium.
If the distribution of formation times is ![]() [the probability of muonium formation between times
[the probability of muonium formation between times
![]() and
and ![]() is
is ![]() ] then
the total polarization at time t is
] then
the total polarization at time t is
After all muonium formation is complete, the resulting
muonium precesses at the same frequency and
undergoes spin relaxation according to the same function
as the prompt muonium fraction.
In this way the long-time muonium ensemble can be characterized
by a single amplitude and phase.
Figure 4.14 shows the asymmetry of the muonium
ensemble (the total muonium signal) in liquid nitrogen at
T=75 K in various transverse magnetic fields,
obtained by fitting the ![]() spectra starting
at t=50 ns.
The solid line is the empirical maximum asymmetry A0
multiplied by the theoretical polarization in Eq. (4.1),
and in which the distribution of formation times is
spectra starting
at t=50 ns.
The solid line is the empirical maximum asymmetry A0
multiplied by the theoretical polarization in Eq. (4.1),
and in which the distribution of formation times is
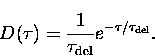
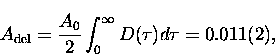
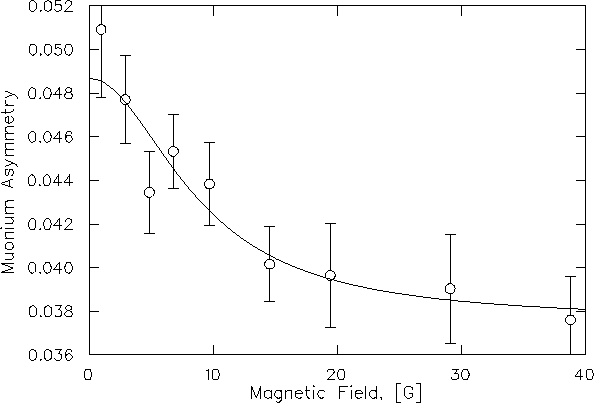 |
Similar experiments on solid nitrogen and rare gas solids have not shown magnetic field dependence of asymmetries, presumably because the time of flight is too short due to greater electron mobility and/or reduced distance.
If the electrons were initially much
further away from the muon than the width of their spatial
distribution, then the maximum muonium formation rate
could be displaced from t=0 by an amount ![]() .In this case, if the prompt muonium had time to precess
one or more full revolutions while the electrons were
diffusing to the muon, the total muonium polarization
would be a periodic function of magnetic field. This
would yield a direct measurement
of the formation time
.In this case, if the prompt muonium had time to precess
one or more full revolutions while the electrons were
diffusing to the muon, the total muonium polarization
would be a periodic function of magnetic field. This
would yield a direct measurement
of the formation time