



Next: Muon decay electron time
Up: Makoto Fujiwara's PhD Thesis
Previous: Implications for our measurements
Muon decay electron time spectrum fit
Fits of muon decay electron time spectra to the exponential functions
were performed taking into account the finite size of the time bins.
For the muon stopping in M different elements, it obviously holds in
the continuous approximation that
where
are the numbers of muons in the element k at time t,
in which the muon disappearance rate is
,
and
.
By solving Eq. C.1 for ,
we have a number of 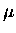 decay per unit time
decay per unit time
where N0k is the number of muons at t=0 in the
element k with
.
Note
that Eq. C.2 can be decomposed into a set of M uncoupled
independent equations.
On the other hand, the decay electron detection rate, which we measure in
our experiments, is
where
is the detector efficiency for decay
electrons from the element k, and
is the branching ratio
of the muon-to-electron decay to total muon disappearance
where
is the muon decay rate in free space, and, for the
element k, Qk is the Huff factor,
the nuclear
capture rate, and
is an effective rate representing
other loss mechanisms such as muon transfer to heavier elements and muonic
atom emission![[*]](foot_motif.gif) .
The Huff factor ()
takes into account the effect of muon binding
to the nucleus, resulting in reduced phase space available as well as the
time dilation of the muon's proper time with respect to the lab frame, both
of which in turn lead to the reduction in muon decay rate, according to
Huff [226]. Thus we have
.
The Huff factor ()
takes into account the effect of muon binding
to the nucleus, resulting in reduced phase space available as well as the
time dilation of the muon's proper time with respect to the lab frame, both
of which in turn lead to the reduction in muon decay rate, according to
Huff [226]. Thus we have
dN^e(t)dt = ddt _k^M N^e_k (t)
& = & _k^M
_k Q_k_0Q_k_0
+ ^C_k +^X_k_k N^0_k
(-_k t)
&=& _k^M _kQ




Next: Muon decay electron time
Up: Makoto Fujiwara's PhD Thesis
Previous: Implications for our measurements
![[*]](foot_motif.gif) .
The Huff factor ()
takes into account the effect of muon binding
to the nucleus, resulting in reduced phase space available as well as the
time dilation of the muon's proper time with respect to the lab frame, both
of which in turn lead to the reduction in muon decay rate, according to
Huff [226]. Thus we have
.
The Huff factor ()
takes into account the effect of muon binding
to the nucleus, resulting in reduced phase space available as well as the
time dilation of the muon's proper time with respect to the lab frame, both
of which in turn lead to the reduction in muon decay rate, according to
Huff [226]. Thus we have