



Next: TOF series B
Up: Yield measurements
Previous: TOFY: Time-of-flight Yield
The measurement for a 3 T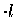 layer in Series A
(
layer in Series A
(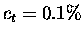 )
had an additional difficulty in the background subtraction,
which was overcome by using different methods of background estimation and
comparing them.
)
had an additional difficulty in the background subtraction,
which was overcome by using different methods of background estimation and
comparing them.
The most suitable background run for the 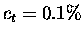 series (BG6 in
Table 8.2, Page
series (BG6 in
Table 8.2, Page ![[*]](cross_ref_motif.gif) ) had rather limited
statistics with about 1/9 of GMUs of the production run. Performing our
standard background subtraction procedure using BG6, illustrated in
Fig. 8.9, exhibited two potential systematic effects:
(a) a Si1 to Si2 detector ratio of up to about 30% was observed in the yield
using BG6 for 3 T
) had rather limited
statistics with about 1/9 of GMUs of the production run. Performing our
standard background subtraction procedure using BG6, illustrated in
Fig. 8.9, exhibited two potential systematic effects:
(a) a Si1 to Si2 detector ratio of up to about 30% was observed in the yield
using BG6 for 3 T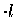 (see values with
in
Table 8.6), which appear to be due mostly to asymmetry
in the background BG6, not the signal, and (b) there appears to be low
energy tails in the background subtracted spectra down to 2 MeV (2000 ch)
(see Fig. 8.9, and Table 8.6).
(see values with
in
Table 8.6), which appear to be due mostly to asymmetry
in the background BG6, not the signal, and (b) there appears to be low
energy tails in the background subtracted spectra down to 2 MeV (2000 ch)
(see Fig. 8.9, and Table 8.6).
Figure:
Si energy spectra for the TOF yield measurement with 3 T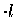 DS D2 in Series A (
DS D2 in Series A (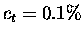 ), with the time cut of 1<t<6
), with the time cut of 1<t<6 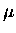 s.
Top figures show the fusion signal (filled circles ) and a background
run BG 6 (open circles), while bottom figures give background
subtracted spectra.
s.
Top figures show the fusion signal (filled circles ) and a background
run BG 6 (open circles), while bottom figures give background
subtracted spectra.
|
Figure 8.10:
The
energy spectra for the TOF 3 T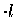 (
(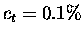 )
measurement
with the background as sum of BG5, 6, and 7, describing Method 2. The
additional correction to the yield in the signal region SG was
applied for the residual background present in the bottom figure,
using the average of the background region B-LO and B-HI. See text
for the details.
)
measurement
with the background as sum of BG5, 6, and 7, describing Method 2. The
additional correction to the yield in the signal region SG was
applied for the residual background present in the bottom figure,
using the average of the background region B-LO and B-HI. See text
for the details.
|
Figure 8.11:
Background subtraction
Method 2-c, where the background
subtracted spectrum obtained using BG5+6+7 (bottom in
Fig. 8.10) was fitted with an
exponential function to remove residual background.
|
Using instead BG5, which does not have DS 500 T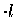 H2 under the DS
deuterium layer, makes the Si1/Si2 ratio consistent with 1. However, the
lack of the H2 layer in BG5 could cause an underestimate of the
background, since muon decay electrons are a major source of background
especially at lower energies. In fact, yields with BG5 are higher than
those with BG6 in all cases, but clearly with a lower energy cut (see
values with
in Table 8.6).
H2 under the DS
deuterium layer, makes the Si1/Si2 ratio consistent with 1. However, the
lack of the H2 layer in BG5 could cause an underestimate of the
background, since muon decay electrons are a major source of background
especially at lower energies. In fact, yields with BG5 are higher than
those with BG6 in all cases, but clearly with a lower energy cut (see
values with
in Table 8.6).
Another possible run to be used for background subtraction is BG7, which
had an emission target with ct=0.2%, and no H2 DS substrate
layer. Despite the difference in ct, which might possibly introduce
further systematic error, this run had much better statistics (about 3
times that of BG6).
Given this situation for the 3 T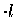 measurement in the
measurement in the 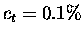 series, we made several different background subtractions, and compared
them to see the systematic effects. Method 1 is the standard procedure
using BG6, but with a wide energy cut (
2.5 < E < 3.7 MeV) to account for
the possibility that the lower energy tails are due indeed to real
series, we made several different background subtractions, and compared
them to see the systematic effects. Method 1 is the standard procedure
using BG6, but with a wide energy cut (
2.5 < E < 3.7 MeV) to account for
the possibility that the lower energy tails are due indeed to real 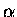 particle events, which gave the Si averaged yield of
/GMU.
particle events, which gave the Si averaged yield of
/GMU.
The energy spectra obtained with Method 1 had nonzero counts even at
energies much higher than the fusion signal, where we expect an average of
counts consistent with zero. In Method 1-b, taking into account the
possibility that this is due to a potential error in the relative
normalization (although the ADC blocking effect in Si detectors was
corrected carefully in Section 8.1.2), we fitted the region
between 4000 and 8000 ch with a constant base line, and subtracted that
from the yield from Method 1 above to obtain
.
Using a line with a slope or exponential curve in the fit gave
a larger base line yield (hence smaller fusion yield), but we use the
value
Ymeth1-b as our upper limit in calculating the average later.
Method 2 used the entire background data set available (sum of BG5, BG6,
and BG7) to make a first order background subtraction (see bottom in
Fig. 8.10). But keeping in mind some differences in the
conditions, we made an additional, second order correction from the above
background. From the narrowly defined signal region (denoted SG,
3.1 <E<
3.7 MeV), the average of counts from the region below (shown as B-LO,
2.2
<E<2.8 MeV) and above (B-HI, 3.8<E<4.6 MeV) were subtracted, i.e.,
Ymeth2 =SG - 0.5(B-LO + B-HI). With SG=
,
B-LO=
,
and B-HI=
,
we have
.
The systematics in Method 2 were checked for the manner in which the
additional correction was made; the background cut, B-LO, might
contain the signal, which, together with the narrow cut for SG, might lead
to over-subtraction of background.
We present two more systematic checks of Method 2, in which the second
order additional correction was done in a different way, while keeping the
first order the same as Method 2.
Method 2-b is simply to use a wider signal region of
2.7 <E< 3.7 MeV, with
B-L0
2.1 <E<2.6 MeV and B-HI
3.8 <E<4.3 MeV. Note that because of the
low energy structure of background, we do not desire to use the spectrum
much lower than 2 MeV. Thus B-LO and B-HI now each have half the energy
width of SG. The detector averaged yield thus obtained with Method 2-b is:
.
In Method 2-c, illustrated in Fig. 8.11, we have fitted
the residual background obtained in Fig. 8.10 with an
exponential function. The fit was performed simultaneously in the regions
B-LO (
2.0 <E<2.4 MeV) and B-HI (
3.8 <E<6.0 MeV), and are plotted with
a solid line in Fig. 8.11. The yield was determined in the
SG region (
2.5 < E< 3.7 MeV), which was excluded from the fit, by
subtracting the area under the fitted curve. We obtain
,
where the error is due to the statistics in the SG
counts.
Table 8.7:
Summary of the detector averaged Si
yield for 3 T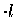 TOF measurement (
TOF measurement (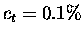 )
with different
background subtraction methods. The energy cut dependent corrections
(cut efficiency and dd proton contribution) are made. Taking the
average of two bold values we obtain
/GMU, without the time cut and the nitrogen contamination
corrections (see text for the details).
)
with different
background subtraction methods. The energy cut dependent corrections
(cut efficiency and dd proton contribution) are made. Taking the
average of two bold values we obtain
/GMU, without the time cut and the nitrogen contamination
corrections (see text for the details).
| Method |
1 |
1-b |
2 |
2-b |
2-c |
| BG run |
BG6 |
BG6 |
BG5+6+7 |
BG5+6+7 |
BG5+6+7 |
| SG cut (MeV) |
2.5; 3.7 |
2.5; 3.7 |
3.1; 3.7 |
2.7; 3.7 |
2.5; 3.7 |
| SG yield (10-6/GMU) |
4.43(26) |
4.43(26) |
4.05(11) |
4.64(14) |
4.81(15) |
| B-LO cut (MeV) |
- |
- |
2.2; 2.8 |
2.1; 2.6 |
2.0; 2.4 |
| B-HI cut (MeV) |
- |
4.0; 8.0 |
3.8; 4.4 |
3.8; 4.3 |
3.8; 6.0 |
| Fit/sum for ith bin |
- |
yi= const. |
|
|
yi=ae-xi/b |
| B yield (10-6/GMU) |
- |
0.38(6) |
0.54(6) |
0.99(11) |
1.36 |
| TOF yield (10-6/GMU) |
4.43(26) |
4.06(27) |
3.52(12) |
3.65(18) |
3.45(15) |
| dd proton |
2.4(9)% |
2.4(9)% |
0 |
2.4(9)% |
2.4(9)% |
| E cut efficiency |
1 |
1 |
0.980(3) |
1 |
1 |
| TOFcorr (10-6/GMU) |
4.32(26) |
3.96(27) |
3.59(12) |
3.56(18) |
3.37(15) |
|
The Si yield for 3 T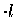 in TOF Series A (
in TOF Series A (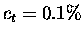 ), using different
background subtraction methods, are summarized in
Table 8.7. Energy cut width dependent corrections, i.e., the energy cut efficiency and the dd proton contribution, which
will be discussed in detail in Sections 8.2.4 and 8.2.3, are
applied here.
), using different
background subtraction methods, are summarized in
Table 8.7. Energy cut width dependent corrections, i.e., the energy cut efficiency and the dd proton contribution, which
will be discussed in detail in Sections 8.2.4 and 8.2.3, are
applied here.
As can be seen, Method 2, 2-b, 2-c, which
all used combined background BG5+6+7 but had different methods of residual
background subtraction, gave consistent results, giving some confidence at
least in the residual background subtraction procedure.
In comparison with Method 1, Method 1-b appears more reliable since it
takes into account the possible relative normalization error by subtracting
a constant base line. Note that in Series B, the constant term was
consistent with zero, as expected. Discarding Method 1, we chose the two
extreme values in (Method 1-b and Method 2-c) as representative of the
deviations due to the background subtraction procedure. Since these
measurements are not completely independent, determining the average and
its error is somewhat tricky. Obviously, since the two values are
incompatible within in the quoted error, simply taking a weighted mean and
combining the error would underestimate the total uncertainty.
Here we adopt a procedure used by the Particle Data
Group [229,230], which scales the error bar
to give
.
In our case, with the numbers
of points and the free parameter being 2 and 1 respectively (hence dof=1),
we scale the error by a factor 1.9 and obtain
/GMU.
As for other TOF series A measurements (with 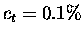 ), the statistics of
the production runs and the standard background run (BG6) are comparable,
and the accuracy is not limited by the background statistics. Also because
of a better signal-to-background ratio, effects of the
background are not as serious. Furthermore, the Si1/Si2 asymmetry in Si
yields are at the 10% level for the most part. Thus, we shall use BG6 for
our background subtraction. Using other backgrounds in fact gives consistent
results for a reasonable range of the energy cuts
(Table 8.6).
), the statistics of
the production runs and the standard background run (BG6) are comparable,
and the accuracy is not limited by the background statistics. Also because
of a better signal-to-background ratio, effects of the
background are not as serious. Furthermore, the Si1/Si2 asymmetry in Si
yields are at the 10% level for the most part. Thus, we shall use BG6 for
our background subtraction. Using other backgrounds in fact gives consistent
results for a reasonable range of the energy cuts
(Table 8.6).




Next: TOF series B
Up: Yield measurements
Previous: TOFY: Time-of-flight Yield
![[*]](cross_ref_motif.gif) ) had rather limited
statistics with about 1/9 of GMUs of the production run. Performing our
standard background subtraction procedure using BG6, illustrated in
Fig. 8.9, exhibited two potential systematic effects:
(a) a Si1 to Si2 detector ratio of up to about 30% was observed in the yield
using BG6 for 3 T
) had rather limited
statistics with about 1/9 of GMUs of the production run. Performing our
standard background subtraction procedure using BG6, illustrated in
Fig. 8.9, exhibited two potential systematic effects:
(a) a Si1 to Si2 detector ratio of up to about 30% was observed in the yield
using BG6 for 3 T