



Next: Analysis II - Emission
Up: Discussion of stopping fraction
Previous: The discrepancy
In an attempt to resolve this discrepancy, we revisit the relative amplitudes
in the telescope measurements. As discussed in Section 6.4.2
(p. ![[*]](cross_ref_motif.gif) ), the telescope data gave some 30% higher
value of the reduced stopping fraction
,
compared to
the electron scintillator data. We suspect that this might be due the
energy sensitivity of the detectors to the stopping fraction, as the
telescope events required a certain energy deposit in the liquid
scintillator. This was experimentally demonstrated in
Fig. 6.6 (page
), the telescope data gave some 30% higher
value of the reduced stopping fraction
,
compared to
the electron scintillator data. We suspect that this might be due the
energy sensitivity of the detectors to the stopping fraction, as the
telescope events required a certain energy deposit in the liquid
scintillator. This was experimentally demonstrated in
Fig. 6.6 (page ![[*]](cross_ref_motif.gif) ), and
qualitatively explained to be due in part to the muon decay electron energy
spectra (p.
), and
qualitatively explained to be due in part to the muon decay electron energy
spectra (p. ![[*]](cross_ref_motif.gif) ).
).
Here we postulate the possibility of muon-capture related processes still
not fully accounted for by various corrections which we have made in
Section 6.4.3. One such example is gamma induced
reactions in the target.
We make use of the minimum ionizing peak (
MeV) in the
telescope energy spectra, and make a comparison with the GEANT simulations
of full electronic processes, to extract the relative amplitude. The
possible advantages of using the energy cuts at this peak, as opposed to no
energy cuts, include: (a) energy deposited from a muon-capture related
process, if it exists, should be less important at high energies, and (b)
with the lack of an energy calibration for the Tel spectra, the minimum
ionizing peak itself can provide a calibration. Nevertheless, in order to
account for some ambiguity![[*]](foot_motif.gif) in the exact cut positions corresponding to the experimental energy cut at
the peak (590<E<790 ch for both Tel1 and Tel2; see
Fig. 6.6), we applied two different sets of cuts in the
Monte Carlo spectra. Shown in Fig. 6.8 are the simulated
spectra and applied cuts. With these cuts, we determined the relative
efficiencies of electron detection necessary to derive the stopping
fraction, as given in Table 6.18. The first
parentheses in the tables are the Monte Carlo statistical errors, while the
second indicate systematic uncertainties due to the different cuts in the
Monte Carlo energy spectra. As can be seen, the resulting relative
efficiencies are not very sensitive to the choice of the cuts. Note that
the charged particle effect ratio
of 1
was used for Tel1 (bold face in the table), as opposed to 1.04 in the
scintillator measurement, because of the higher energy cuts applied here.
The stopping fractions
SARH determined with the telescope thus are
given in Table 6.19, together with uncorrected values.
in the exact cut positions corresponding to the experimental energy cut at
the peak (590<E<790 ch for both Tel1 and Tel2; see
Fig. 6.6), we applied two different sets of cuts in the
Monte Carlo spectra. Shown in Fig. 6.8 are the simulated
spectra and applied cuts. With these cuts, we determined the relative
efficiencies of electron detection necessary to derive the stopping
fraction, as given in Table 6.18. The first
parentheses in the tables are the Monte Carlo statistical errors, while the
second indicate systematic uncertainties due to the different cuts in the
Monte Carlo energy spectra. As can be seen, the resulting relative
efficiencies are not very sensitive to the choice of the cuts. Note that
the charged particle effect ratio
of 1
was used for Tel1 (bold face in the table), as opposed to 1.04 in the
scintillator measurement, because of the higher energy cuts applied here.
The stopping fractions
SARH determined with the telescope thus are
given in Table 6.19, together with uncorrected values.
Table 6.18:
The
correction factors  ,
,
 in Eq. 6.15,
and assumed quantities for the derivation by
Eqs. 6.16, 6.17. Values with `*' are
taken from the ratio of the efficiencies calculated by GEANT
simulation with the cuts given in Fig 6.8. The
first parentheses are the Monte Carlo statistical errors, while
the second indicate systematic uncertainties due to the different
cuts.
in Eq. 6.15,
and assumed quantities for the derivation by
Eqs. 6.16, 6.17. Values with `*' are
taken from the ratio of the efficiencies calculated by GEANT
simulation with the cuts given in Fig 6.8. The
first parentheses are the Monte Carlo statistical errors, while
the second indicate systematic uncertainties due to the different
cuts.
| Detector |
|
|
|
 |
 |
|
| Tel1 |
0.600(9)(9)* |
1 |
1 |
0.510(8)(8) |
1.059(18)(5)* |
|
| Tel2 |
0.578(12)(7)* |
1 |
1 |
0.491(10)(6) |
1.188(25)(4)* |
|
|
Table 6.19:
The uncorrected
stopping fraction
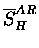 and the corrected one
SHAR using the minimum ionizing
peak of the telescope detectors in the relative amplitude
method. Uncorrected values with nominal energy cuts
(200<E<1200 ch) are also given for comparison.
and the corrected one
SHAR using the minimum ionizing
peak of the telescope detectors in the relative amplitude
method. Uncorrected values with nominal energy cuts
(200<E<1200 ch) are also given for comparison.
| |
Energy cuts (%) |
Tel1 |
Tel2 |
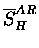 |
nominal |
36.3(4) |
32.8(4) |
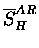 |
min. ion. peak |
42.4(8) |
39.9(7) |
|
SHAR |
min. ion. peak |
31.3(14) |
29.6(14) |
|
The results for
SARH from the telescope are in good agreement with
the absolute amplitude method, while in disagreement with the relative
method with the scintillators. The stopping fractions determined from
various methods are summarized in Table 6.20. Also listed
is the result of a GEANT based beam stopping simulation performed by
Marshall assuming the peak momentum of 27.0 MeV/c with
(these values were carefully tuned to match the relative hydrogen stopping
fractions for a range of beam momentum). Our results suggest that the
relative amplitude method, using electron scintillators, may be unreliable
for a stopping fraction determination, even with elaborate corrections
applied as in the preceding sections, due perhaps to further capture
related background such as nuclear gammas which are not accounted for. In
fact, a preliminary study by Art Olin using an evaporation model for
particle emission following nuclear excitation from muon capture suggests
this may be the case. Excluding the scintillator relative amplitude values,
we obtain consistent results on the stopping fraction. The absolute
amplitude method with its advantages discussed above,
appears to be more reliable, hence I shall use the value
for the present work.
Table 6.20:
Summary of stopping fractions determined via various methods. The
absolute amplitude result (bold face) will be used for this work.
| Method |
Detector |
SH (%) |
Comment |
| Relative amplitude |
En2 |
23.4(7) |
 capture related background?
capture related background? |
| Relative amplitude |
Tel1, 2 |
30.5(14) |
Energy cut  16-20 MeV 16-20 MeV |
| (min. ionizing peak) |
|
|
|
| Absolute amplitude |
En2, Tel2 |
29.9(15) |
No MC correction necessary |
| Beam simulation |
(GEANT) |
31.1 |
p=27.0 MeV/c,
% |
|
Finally, I point out that since many of the previous experiments in the
field used the simple relative amplitude method, often without any
efficiency corrections, their results may require some re-interpretation,
particularly when muon stopping in non-hydrogenic materials is significant,
as in a low density gas target.




Next: Analysis II - Emission
Up: Discussion of stopping fraction
Previous: The discrepancy
![[*]](cross_ref_motif.gif) ), the telescope data gave some 30% higher
value of the reduced stopping fraction
,
compared to
the electron scintillator data. We suspect that this might be due the
energy sensitivity of the detectors to the stopping fraction, as the
telescope events required a certain energy deposit in the liquid
scintillator. This was experimentally demonstrated in
Fig. 6.6 (page
), the telescope data gave some 30% higher
value of the reduced stopping fraction
,
compared to
the electron scintillator data. We suspect that this might be due the
energy sensitivity of the detectors to the stopping fraction, as the
telescope events required a certain energy deposit in the liquid
scintillator. This was experimentally demonstrated in
Fig. 6.6 (page ![[*]](cross_ref_motif.gif) ), and
qualitatively explained to be due in part to the muon decay electron energy
spectra (p.
), and
qualitatively explained to be due in part to the muon decay electron energy
spectra (p. ![[*]](cross_ref_motif.gif) ).
).
![[*]](foot_motif.gif)