

Next: Kerr Black Holes
Up: Black Holes
Previous: Black Holes
One of the interesting features of general relativity
is that time slows down as you approach the
Schwarzschild radius of a black hole. Not to you,
of course; your subjective experience of time is unaffected,
but an outside observer would see your clock moving slower and
slower (and turning redder and redder) as you fell into the
black hole, until (paradoxically) you stopped completely
(and were red-shifted out of sight) at 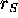 .
Your own experience would depend upon the mass
of the black hole. If it were big enough, the trip
in free fall through
.
Your own experience would depend upon the mass
of the black hole. If it were big enough, the trip
in free fall through 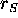 would be
rather uneventful -
you wouldn't notice much of anything unusual, unless of course
you tried to get out again. If, on the other hand, you approached
a small black hole, the tidal forces
[the gravitational gradient ] would tear you apart
before you even reached
would be
rather uneventful -
you wouldn't notice much of anything unusual, unless of course
you tried to get out again. If, on the other hand, you approached
a small black hole, the tidal forces
[the gravitational gradient ] would tear you apart
before you even reached 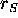 . This has
some interesting
consequences which I will discuss later.
. This has
some interesting
consequences which I will discuss later.
The transformation between ``outside'' and ``inside''
coordinates has an interesting feature: while it is strictly impossible
for anything inside 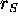 to
come out,
one can imagine extending the mathematics of the relativistic transformation
from outside to inside, at least formally. The result would be that
``inside time'' is in the opposite direction
from ``outside time.'' This would mean that what we see as
matter falling inexorably into a black hole
must ``look'' to the interior inhabitants (if any) like
an expansion of matter away from the singularity
- a sort of Big Bang. Which raises an interesting
question about our Big Bang: are we inside a
black hole in someone else's Universe? Hmm....
And are the black holes in our Universe
time-reversed Big Bangs for the inhabitants (if any)
of their interiors? Hmmmmmm....
Unfortunately, this sophistry is probably all wrong.
If you want a proper, correct and comprehensible
description of phenomena at the Schwarzschild radius,
go talk to Bill Unruh!
to
come out,
one can imagine extending the mathematics of the relativistic transformation
from outside to inside, at least formally. The result would be that
``inside time'' is in the opposite direction
from ``outside time.'' This would mean that what we see as
matter falling inexorably into a black hole
must ``look'' to the interior inhabitants (if any) like
an expansion of matter away from the singularity
- a sort of Big Bang. Which raises an interesting
question about our Big Bang: are we inside a
black hole in someone else's Universe? Hmm....
And are the black holes in our Universe
time-reversed Big Bangs for the inhabitants (if any)
of their interiors? Hmmmmmm....
Unfortunately, this sophistry is probably all wrong.
If you want a proper, correct and comprehensible
description of phenomena at the Schwarzschild radius,
go talk to Bill Unruh!


Next: Kerr Black Holes
Up: Black Holes
Previous: Black Holes
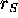 .
Your own experience would depend upon the mass
of the black hole. If it were big enough, the trip
in free fall through
.
Your own experience would depend upon the mass
of the black hole. If it were big enough, the trip
in free fall through 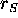 would be
rather uneventful -
you wouldn't notice much of anything unusual, unless of course
you tried to get out again. If, on the other hand, you approached
a small black hole, the tidal forces
[the gravitational gradient ] would tear you apart
before you even reached
would be
rather uneventful -
you wouldn't notice much of anything unusual, unless of course
you tried to get out again. If, on the other hand, you approached
a small black hole, the tidal forces
[the gravitational gradient ] would tear you apart
before you even reached 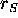 . This has
some interesting
consequences which I will discuss later.
. This has
some interesting
consequences which I will discuss later.


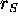 to
come out,
one can imagine extending the mathematics of the relativistic transformation
from outside to inside, at least formally. The result would be that
``inside time'' is in the opposite direction
from ``outside time.'' This would mean that what we see as
matter falling inexorably into a black hole
must ``look'' to the interior inhabitants (if any) like
an expansion of matter away from the singularity
- a sort of Big Bang. Which raises an interesting
question about our Big Bang: are we inside a
black hole in someone else's Universe? Hmm....
And are the black holes in our Universe
time-reversed Big Bangs for the inhabitants (if any)
of their interiors? Hmmmmmm....
Unfortunately, this sophistry is probably all wrong.
If you want a proper, correct and comprehensible
description of phenomena at the Schwarzschild radius,
go talk to Bill Unruh!
to
come out,
one can imagine extending the mathematics of the relativistic transformation
from outside to inside, at least formally. The result would be that
``inside time'' is in the opposite direction
from ``outside time.'' This would mean that what we see as
matter falling inexorably into a black hole
must ``look'' to the interior inhabitants (if any) like
an expansion of matter away from the singularity
- a sort of Big Bang. Which raises an interesting
question about our Big Bang: are we inside a
black hole in someone else's Universe? Hmm....
And are the black holes in our Universe
time-reversed Big Bangs for the inhabitants (if any)
of their interiors? Hmmmmmm....
Unfortunately, this sophistry is probably all wrong.
If you want a proper, correct and comprehensible
description of phenomena at the Schwarzschild radius,
go talk to Bill Unruh!