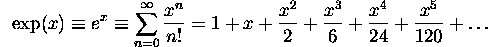
It is helpful to remember the definition of the exponential function in terms of a power series:
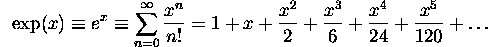
If we let x be imaginary,
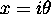 (where
(where 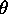 is real),
then this can be written
is real),
then this can be written
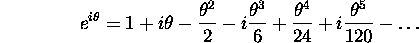
which ought to remind you (doesn't it?) of the series expansions for the sinusoidal functions:
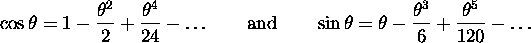
Note that these expansions perform a sort of ``leapfrog'' between even and odd terms. Putting them all together we can easily see that
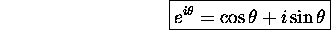
and, since 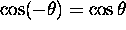 while
while
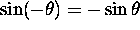 ,
,
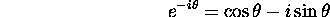
These simple equivalences are, to my mind, among the most
astonishing relationships in all of mathematics.
Why? Because they show an intimate relationship
between two functions which would seem at first glance
to have absolutely nothing in common: the monotonically
increasing or decreasing exponential function
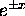 and the sinusoidally oscillating
and the sinusoidally oscillating
 and
and
 functions!
functions!
We can also invert the relationship and obtain a definition
for the 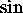 and
and
 functions in terms of exponentials:
functions in terms of exponentials:
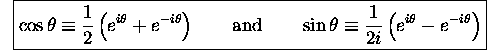
Let's review the most important (for Physics, anyway)
property of the exponential function: it is its own derivative!
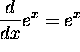 .
If x = kt then we ``pull out an extra factor of k''
with each derivative with respect to t:
.
If x = kt then we ``pull out an extra factor of k''
with each derivative with respect to t:

This latter property (which, by the way, works just as well
for complex k as for real k)
establishes the connection between
the derivatives of
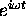 (for instance) and those of
(for instance) and those of
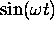 and
and
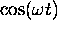 :
:
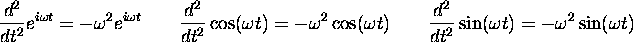
You will recall how useful these second-derivative properties were in simple harmonic motion and waves. Well, you ain't seen nothing yet!