We can expand the potential function ![]() in a Taylor series around
some
point in space
in a Taylor series around
some
point in space ![]() to give the potential at the six points
to give the potential at the six points
![]() ,
, ![]() and
and ![]() which symmetrically surround
which symmetrically surround ![]() .
.
To third order in ![]() (i.e.
(i.e. ![]() ):
):
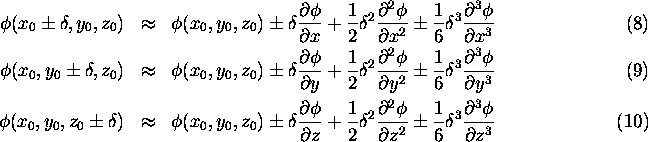
The average of those six values of the potential at points surrounding
![]() is then, to third order
in
is then, to third order
in ![]() :
:
![]()
If the potential satisfies Laplace's equation ![]() ,
then the average of the six neighbouring values of the potential is just the
potential at the point
in question (where we have neglected terms in
,
then the average of the six neighbouring values of the potential is just the
potential at the point
in question (where we have neglected terms in ![]() and higher).
and higher).
We can now use this result to calculate the potential ![]() numerically
for a given set of
boundary conditions. We rely on the fact (demonstrated above) that the value of
a harmonic function
at some point in space is equal to its average over the neighbourhood of the
point. We represent
the potential function
numerically
for a given set of
boundary conditions. We rely on the fact (demonstrated above) that the value of
a harmonic function
at some point in space is equal to its average over the neighbourhood of the
point. We represent
the potential function ![]() by values at an array of discrete points,
including discrete points
at the boundaries. We then adjust the values at non-boundary points until each
value is equal to the average of
its neighbouring values. To do this, we employ an approximate technique: the
relaxation method.
by values at an array of discrete points,
including discrete points
at the boundaries. We then adjust the values at non-boundary points until each
value is equal to the average of
its neighbouring values. To do this, we employ an approximate technique: the
relaxation method.
We start with the boundary values fixed at their given values and assign arbitrary values to the interior points. Next, we cycle through each of the interior points and assign its value to the average of its neighbouring 4 (in two dimensions) adjacent grid points. We repeat this over and over again until the changes in the values become acceptably small. We could do this calculation by hand, though we would quickly find the iterations quite tiresome. Fortunately, we can use a spreadsheet program to quickly do these calculations for us.