



Next: Coupled rearrangement channel method
Up: Variational approaches
Previous: Variational approaches
A popular choice are Hylleraas type
functions [106,107,108,109], which for J=0 states read
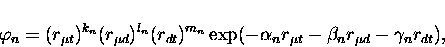 |
(34) |
and are expressed in the interparticle co-ordinates, where
rxy denotes the distance between the particle x and y. The
exponential parameters
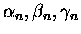 are often
taken to be the same for all n to reduce the number of parameters to be
optimized. For loosely bound states (1,1) of
are often
taken to be the same for all n to reduce the number of parameters to be
optimized. For loosely bound states (1,1) of 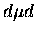 and
and 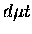 ,
similar functions with
ki=li=mi, known as Slater gemials were
found to be more useful in representing the large physical size of the
states [110,84]. The disadvantage with Slater gemials is that
one has to optimize a large number of exponential parameters, which is very
time consuming. Another disadvantage is its ``linear dependencies''
problem. This is due to the fact that the basis in this set is nearly
linearly dependent,
i.e. rather non-orthogonal. Since the functions differ only by their
exponents, an optimized basis set sometimes has several functions with
close values of the exponents [85]. Thus, the use of extended
arithmetic precision (
,
similar functions with
ki=li=mi, known as Slater gemials were
found to be more useful in representing the large physical size of the
states [110,84]. The disadvantage with Slater gemials is that
one has to optimize a large number of exponential parameters, which is very
time consuming. Another disadvantage is its ``linear dependencies''
problem. This is due to the fact that the basis in this set is nearly
linearly dependent,
i.e. rather non-orthogonal. Since the functions differ only by their
exponents, an optimized basis set sometimes has several functions with
close values of the exponents [85]. Thus, the use of extended
arithmetic precision (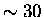 decimal digits) is necessary.
decimal digits) is necessary.




Next: Coupled rearrangement channel method
Up: Variational approaches
Previous: Variational approaches