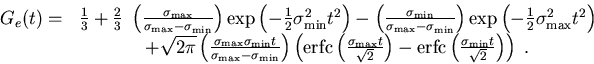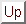

Next: (Gaussian)x(power) distribution of Gaussians
Up: Between Gaussian and Lorentzian
Previous: Pearson from Gaussian
Figure 2:
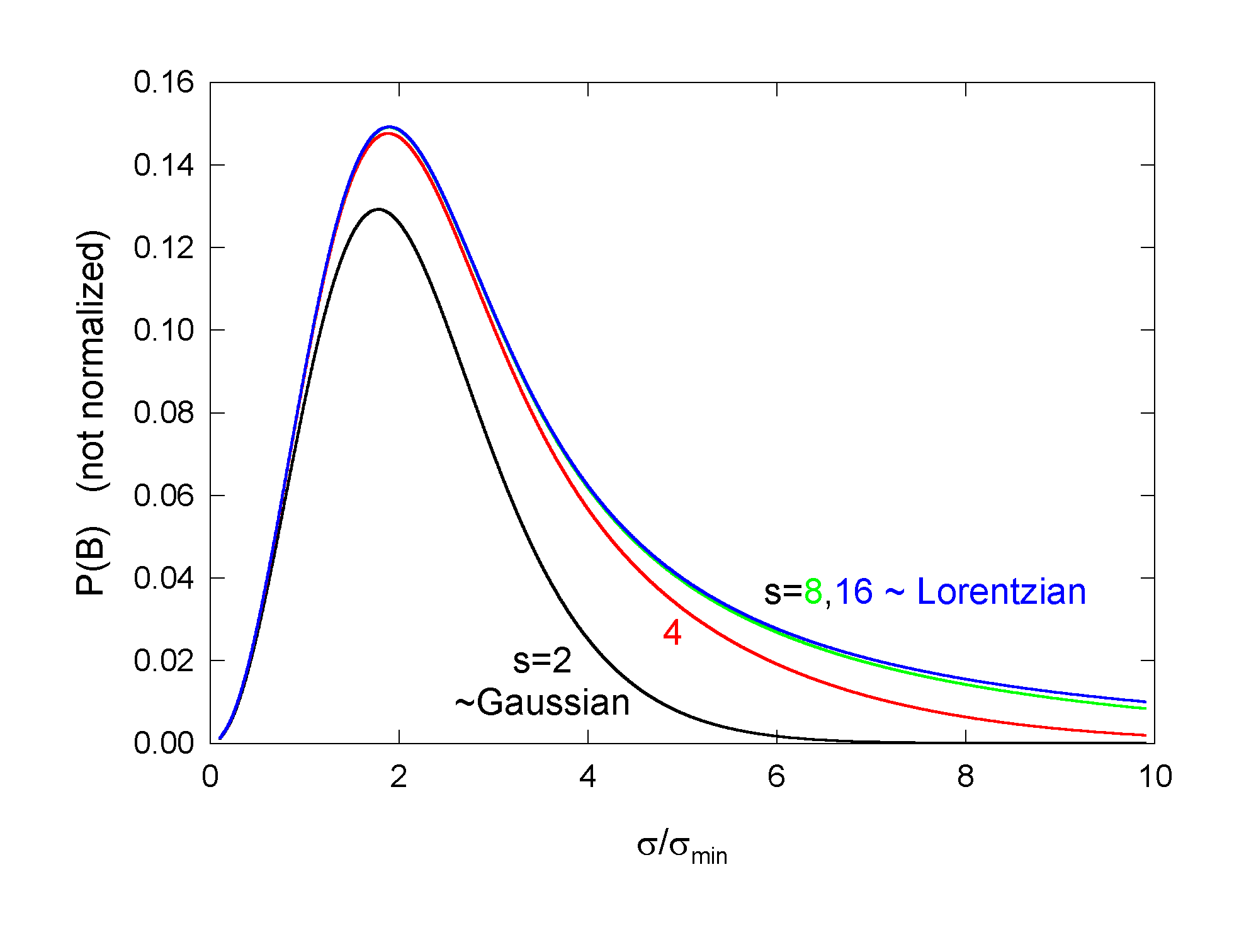
Let
Then, convoluting with Gaussian,
and
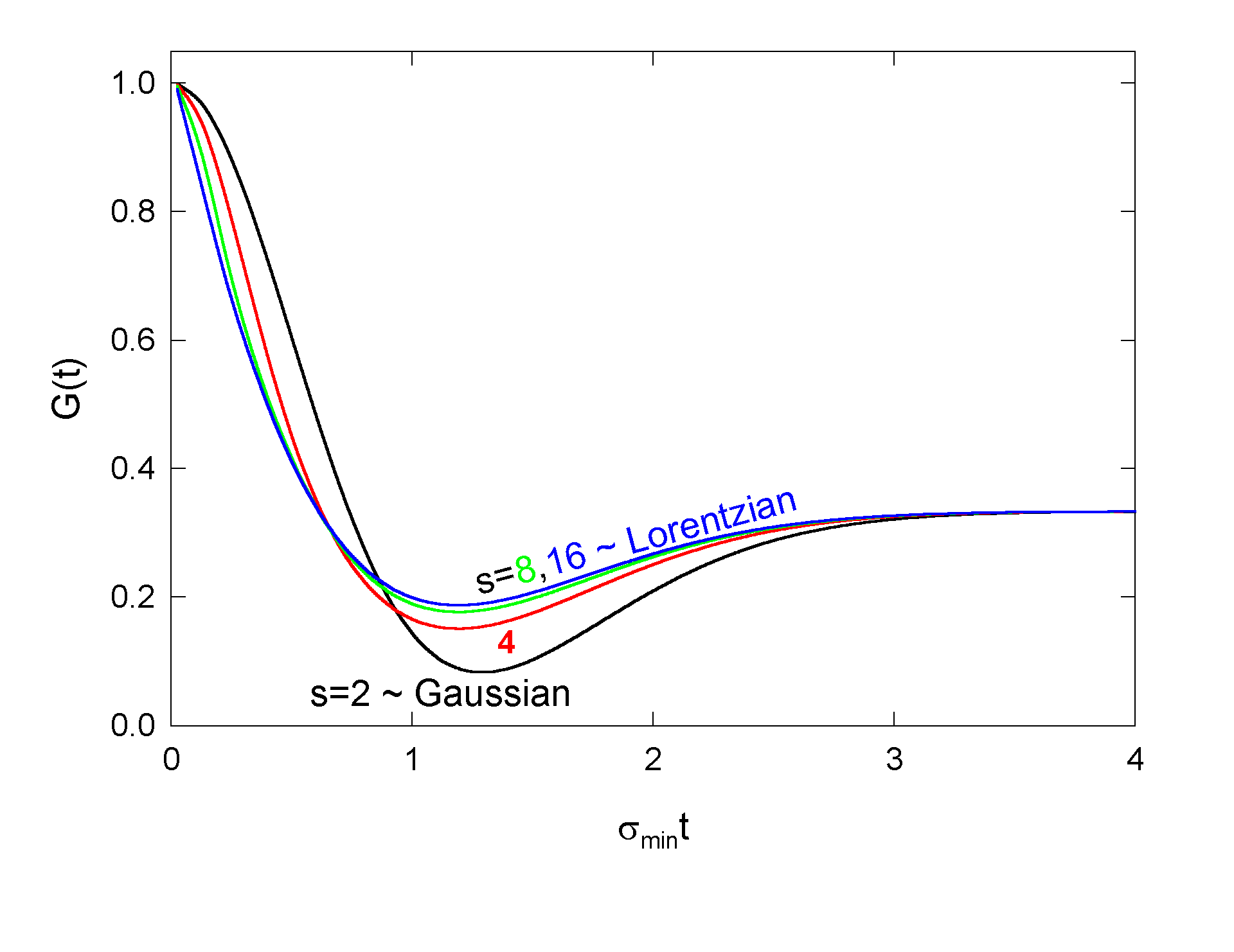
Figure 3:
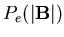 is shown for a variety of
is shown for a variety of
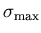 values while
keeping
values while
keeping
 constant in Fig.2, and similarly Ge(t) in
Fig.3. As
constant in Fig.2, and similarly Ge(t) in
Fig.3. As
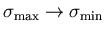 ,
,
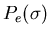 becomes trivial, so all the distributions and the relaxation function tend
to Gaussian in that limit. As
becomes trivial, so all the distributions and the relaxation function tend
to Gaussian in that limit. As
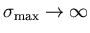 for
finite nonzero
for
finite nonzero
 ,
the distributions and the relaxation
function evolve in a Lorentzian-like direction, but even in the limit, they
do not quite get there. The depth of the minimum of the limit relaxation
function is significantly deeper than the minimum of the Lorentzian
Kubo-Toyabe. At the limit,
,
the distributions and the relaxation
function evolve in a Lorentzian-like direction, but even in the limit, they
do not quite get there. The depth of the minimum of the limit relaxation
function is significantly deeper than the minimum of the Lorentzian
Kubo-Toyabe. At the limit,
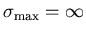 ,
the "Lorentzian
pathology'' does develop: the second moments of the distributions diverge,
and the relaxation function develops a slope at t=0. Note that taking
,
the "Lorentzian
pathology'' does develop: the second moments of the distributions diverge,
and the relaxation function develops a slope at t=0. Note that taking
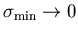 for any fixed value of
for any fixed value of
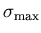 makes
the distributions' norms diverge, and drives
makes
the distributions' norms diverge, and drives
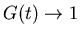 .
.


Next: (Gaussian)x(power) distribution of Gaussians
Up: Between Gaussian and Lorentzian
Previous: Pearson from Gaussian
Jess H. Brewer
2002-09-24


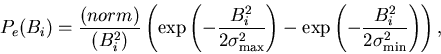
![\begin{displaymath}P_e(\vert{\bf B}\vert)=\frac{(norm)}{B^2}\left[ \left( 1+\fra . . .
. . . exp \left( -\frac{B^2}{2\sigma _{\min
}^2}\right) \right] ,
\end{displaymath}](img22.gif)