In a hydrogen atom the electron and proton spins
can combine in four ways:
the SINGLET state
![]() has an energy
has an energy
![]() J
below the three TRIPLET states
J
below the three TRIPLET states
![]() ,
,
![]() and
and ![]() which are degenerate in zero magnetic field.
The energies of the singlet and triplet
which are degenerate in zero magnetic field.
The energies of the singlet and triplet ![]() states
are not shifted much by a weak magnetic field
states
are not shifted much by a weak magnetic field
![]() (where
(where ![]() is the magnitude of the [negative] magnetic moment
of the triplet state),
but the
is the magnitude of the [negative] magnetic moment
of the triplet state),
but the
![]() states split by
states split by
 1,±1
= ±mB.
1,±1
= ±mB.
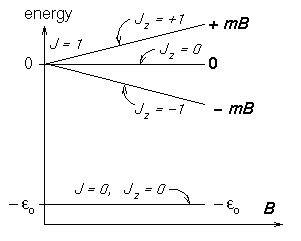
- [20 marks]
In the limit of zero magnetic field,
what fraction of an ensemble of H atoms
is in the singlet state
in thermal equilibrium at a temperature of
100 mK [0.1 K]?
ANSWER: This is a simple Boltzmann distribution: probability of singlet state
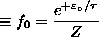 where
where
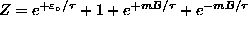 is the
partition function. For B=0,
is the
partition function. For B=0,
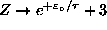 , giving
, giving
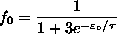 .
At
.
At
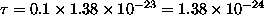 J,
J,
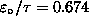 and
and
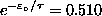 ,
giving
,
giving
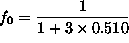 or
or
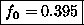 = fraction of atoms in the singlet state.
= fraction of atoms in the singlet state.
- [15 marks]
Derive an expression for the polarization
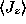 of an ensemble of H atoms in a weak magnetic field
of an ensemble of H atoms in a weak magnetic field
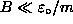 in thermal equilibrium
at a temperature
in thermal equilibrium
at a temperature
 . Express your answer
in terms of
. Express your answer
in terms of
 , m, B and
, m, B and
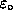 .
.
ANSWER:
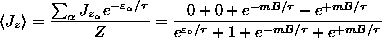 or
or
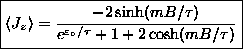 .
.
- [15 marks]
Discuss the behaviour of
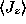 as
as
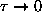 and as
and as
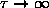 .
.
ANSWER: As
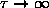 ,
,
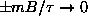 and
the exponentials all approach unity; the two in
the numerator cancel, giving
and
the exponentials all approach unity; the two in
the numerator cancel, giving
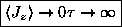 .
As
.
As
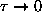 ,
,
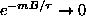 and
and
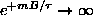 . However, since
. However, since
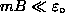 ,
,
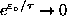 even faster, so
even faster, so
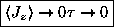 .
Of course, in between
.
Of course, in between
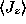 must have
nonzero values and there must be a peak in the magnitude
somewhere. This could be found by differentiating
with respect to
must have
nonzero values and there must be a peak in the magnitude
somewhere. This could be found by differentiating
with respect to
 and setting the derivative
equal to zero, but this was not requested.
An example is shown below for the case of
and setting the derivative
equal to zero, but this was not requested.
An example is shown below for the case of
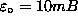 .
.

- [10 marks]
Show that the average number of identical fermions
in a given state of energy
 in thermal and diffusive equilibrium with a reservoir
at temperature
in thermal and diffusive equilibrium with a reservoir
at temperature
 and chemical potential
and chemical potential
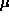 is
is
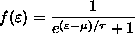
ANSWER: This is easy if we apply the principles of diffusive equilibrium to a given single-particle state of energy
 :
it may be populated by either one particle (N=1)
or none (N=0); all other values of N are explicitly
forbidden by the Pauli principle. We use
:
it may be populated by either one particle (N=1)
or none (N=0); all other values of N are explicitly
forbidden by the Pauli principle. We use
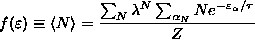 ,
where is the Gibbs sum. In this case,
,
where is the Gibbs sum. In this case,
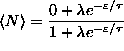
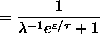 .
Since
.
Since
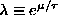 this gives
this gives
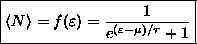 .
.
- [20 marks]
On one graph, sketch f as a function of
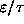 from 0 to
from 0 to
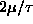 for two cases:
for two cases:
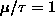 and
and
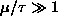 .
[Hint: Let
.
[Hint: Let
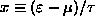 and estimate f at x=0,
and estimate f at x=0,
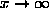 and
and
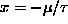 , its minimum value.]
, its minimum value.]
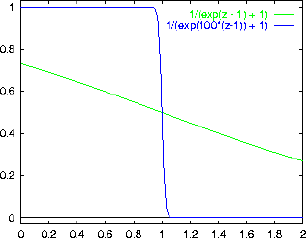
ANSWER: The graph below shows f as a function of
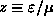 (i.e.
(i.e.
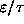 in units of
in units of
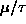 ) for
) for
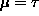 and for
and for
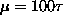 .
For z=1
(
.
For z=1
(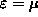 or x=0)
we always get
or x=0)
we always get
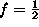 and for
and for 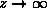 (same as
(same as
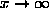 or
or
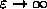 ) we always get
) we always get
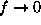 .
For
.
For
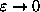 (same as
(same as
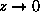 or
or
 )
we get
)
we get
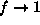 if
if
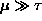 and
and
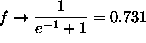 if
if
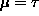 . That case
(
. That case
(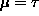 ) also gives
f = 0.119 at
) also gives
f = 0.119 at
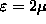 (z=2), as shown.
The main thing to realize here is that
(z=2), as shown.
The main thing to realize here is that
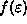 becomes more and more like a step function
as
becomes more and more like a step function
as
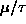 gets larger and larger (i.e. at low temperature).
gets larger and larger (i.e. at low temperature).
- [10 marks]
Describe in words what the preceding results tell us
about the occupation of various states at
 .
.
ANSWER: At
 the distribution becomes a simple step function
at
the distribution becomes a simple step function
at
 :
all states below the Fermi energy
:
all states below the Fermi energy
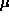 are filled (N=1) and all states above
are filled (N=1) and all states above
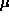 are empty (N=0).
are empty (N=0).
- [10 marks]
Now suppose that N indentical spin-1/2 fermions
are placed in the same parabolic potential well
(simple harmonic oscillator) with fundamental frequency
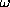 .
Assume that the fermions do not interact with each other
and that
.
Assume that the fermions do not interact with each other
and that 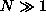 .
What is their chemical potential
at zero temperature (also known as the
FERMI
ENERGY)?
.
What is their chemical potential
at zero temperature (also known as the
FERMI
ENERGY)?
ANSWER: Of the many ways to approach this part, the easiest is to just think about it! Since the chemical potential is the incremental change in free energy as the last particle is added (
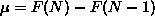 ),
and the free energy
),
and the free energy
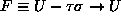 at
at
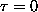 ,
,
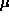 is just the energy level at which the last particle
goes in. For spin-1/2 particles, two can go into each state
(
is just the energy level at which the last particle
goes in. For spin-1/2 particles, two can go into each state
(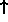 and
and
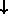 ) and the states
are evenly spaced,
) and the states
are evenly spaced,
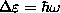 ,
so the last particle goes in at
,
so the last particle goes in at
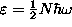 and that is the chemical potential at
and that is the chemical potential at
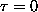 or FERMI
ENERGY:
or FERMI
ENERGY:
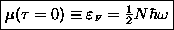 .
.
Note: it has been brought to my attention that some people had seen a derivation of the Fermi-Dirac distribution function before, while others had not; this was correlated with which Engineering specialization people had been following. Since this question is easy to answer if you grasp the basic approach and almost impossible to solve by plugging in standard formulas, it was an excellent test of your ability to synthesize ideas (the whole point of a Physics education) but an unfair one because of the importance of ``prior knowledge.'' I will try to take this into account when making up final marks, by noting which programs people are in and which courses you have taken previously. I may need to get that information from you on the Web.