


Next: Ginzburg-Landau Theory
Up: Superconductivity
Previous: London Theory
BCS theory explains the occurrence of
superconductivity quantum mechanically through the
interaction of electrons and phonons [14][15].
One electron pulls in nearby
positive ions, generating a local excess positive charge which then draws a
second electron towards the first. This attraction leads to
the formation of Cooper pairs. These are bound states composed of
two electrons whose momenta each exceed the Fermi momentum pF while their
combined energy, both potential and kinetic, has fallen to less than 2EF.
Although these two electrons continually scatter each other to new individual
momenta, the total momentum of each Cooper pair is unchanging and identical.
The net energy of a Cooper pair is lowest when it possesses zero momentum
and the electrons comprising it have opposite spins. The BCS cutoff
stipulates that the attraction needed to create Cooper pairs transpires only
between electrons within a Debye energy
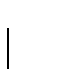 of the Fermi level EF.
For this reason the number of scattering processes allowed to the electrons
of a Cooper pair, and consequently the amount by which their total energy
decreases, is sharply maximal when their centre of mass is stationary. The
existence of more Cooper pairs leaves fewer momentum states available for
scattering into, diminishing the negative potential energy associated with
the attractive interaction. The BCS ground state
contains as many Cooper pairs as can form with a negative potential energy
of greater magnitude than the requisite kinetic energy increment. This
achieves the lowest possible total energy of all the electrons. Exciting
a superconductor to higher states necessitates one or more Cooper pairs
breaking up.
of the Fermi level EF.
For this reason the number of scattering processes allowed to the electrons
of a Cooper pair, and consequently the amount by which their total energy
decreases, is sharply maximal when their centre of mass is stationary. The
existence of more Cooper pairs leaves fewer momentum states available for
scattering into, diminishing the negative potential energy associated with
the attractive interaction. The BCS ground state
contains as many Cooper pairs as can form with a negative potential energy
of greater magnitude than the requisite kinetic energy increment. This
achieves the lowest possible total energy of all the electrons. Exciting
a superconductor to higher states necessitates one or more Cooper pairs
breaking up.
The dissociation of a Cooper pair yields two quasiparticles [14].
These are electrons no longer restrained to occupy states of equal and
opposite momenta. BCS theory proposes that splitting up a Cooper pair needs
at least an energy 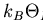 .
This added energy supplies the binding
energy of the Cooper pair and lifts the total energy of all the electrons.
Consequently no quasiparticle energy levels exist within a
BCS energy gap
.
This added energy supplies the binding
energy of the Cooper pair and lifts the total energy of all the electrons.
Consequently no quasiparticle energy levels exist within a
BCS energy gap 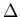 of the Fermi energy EF. The states absent from
this energy region reside at its upper bound
of the Fermi energy EF. The states absent from
this energy region reside at its upper bound
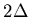 ,
creating there a
peak in the density of states N(E) [16]. As the temperature Trises, the BCS energy gap
,
creating there a
peak in the density of states N(E) [16]. As the temperature Trises, the BCS energy gap 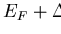 shrinks in all k-space
directions [17] and thermally excited quasiparticles become more
numerous.
shrinks in all k-space
directions [17] and thermally excited quasiparticles become more
numerous.
The BCS energy gap 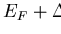 is an important superconducting parameter.
A spherically symmetric gap
is an important superconducting parameter.
A spherically symmetric gap 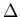 is termed s-wave pairing, while one with
the symmetry of the crystal is known as anisotropic s-wave pairing.
Unconventional pairing results from interactions other than that between
electrons and phonons. This produces gap
is termed s-wave pairing, while one with
the symmetry of the crystal is known as anisotropic s-wave pairing.
Unconventional pairing results from interactions other than that between
electrons and phonons. This produces gap 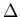 symmetries lower than that
of the crystal [16], for example an energy gap
symmetries lower than that
of the crystal [16], for example an energy gap 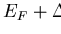 with
nodal lines. Through the relation [18]
with
nodal lines. Through the relation [18]
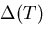 |
(4.9) |
where vF is the Fermi velocity, the BCS energy gap 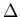 provides
an estimate of the scale
provides
an estimate of the scale 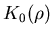 of the spatial correlation of the
superelectrons. This characteristic range
of the spatial correlation of the
superelectrons. This characteristic range 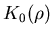 is called the
BCS coherence length. The BCS energy gap
is called the
BCS coherence length. The BCS energy gap 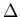 turns out to be
directly proportional to the order parameter
turns out to be
directly proportional to the order parameter 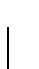 of the Ginzburg-Landau
theory.
of the Ginzburg-Landau
theory.



Next: Ginzburg-Landau Theory
Up: Superconductivity
Previous: London Theory
Jess H. Brewer
2001-10-31
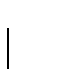 of the Fermi level EF.
For this reason the number of scattering processes allowed to the electrons
of a Cooper pair, and consequently the amount by which their total energy
decreases, is sharply maximal when their centre of mass is stationary. The
existence of more Cooper pairs leaves fewer momentum states available for
scattering into, diminishing the negative potential energy associated with
the attractive interaction. The BCS ground state
contains as many Cooper pairs as can form with a negative potential energy
of greater magnitude than the requisite kinetic energy increment. This
achieves the lowest possible total energy of all the electrons. Exciting
a superconductor to higher states necessitates one or more Cooper pairs
breaking up.
of the Fermi level EF.
For this reason the number of scattering processes allowed to the electrons
of a Cooper pair, and consequently the amount by which their total energy
decreases, is sharply maximal when their centre of mass is stationary. The
existence of more Cooper pairs leaves fewer momentum states available for
scattering into, diminishing the negative potential energy associated with
the attractive interaction. The BCS ground state
contains as many Cooper pairs as can form with a negative potential energy
of greater magnitude than the requisite kinetic energy increment. This
achieves the lowest possible total energy of all the electrons. Exciting
a superconductor to higher states necessitates one or more Cooper pairs
breaking up.