



Next: Variational approaches
Up: Adiabatic approaches
Previous: Multi-level calculations
Improved Adiabatic methods
The difficulties associated with the Adiabatic Representation method have
been discussed by many authors (for example, see Ref. [102]).
Ponomarev summarizes its disadvantages in treating boundary
conditions [103,104]:
- 1.
- Incorrect dissociation limit of the system
 ,
when it
decays into
,
when it
decays into
 and
and
 .
.
- 2.
- Incorrect value of momentum in the reaction channels.
- 3.
- Infinite and long-range behavior of the non-diagonal potential
Uij(R) as
 .
.
Cohen and his co-workers at Los Alamos used what they call the ``Improved
Adiabatic'' approach [105] to address some of the above
limitations. In the standard Adiabatic Representation method, the
Hamiltonian was separated into two parts (Eq. 2.5); the zero
order term describing the two centre Coulomb problem (
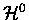 TC), and the perturbative term for the relative motions of the
nuclei as well as nuclear-muonic motion coupling (
TC), and the perturbative term for the relative motions of the
nuclei as well as nuclear-muonic motion coupling (
 ).
In the asymmetric nuclear system (e.g.,
Ma > Mb), since infinite
mass for both the nuclei is assumed in
).
In the asymmetric nuclear system (e.g.,
Ma > Mb), since infinite
mass for both the nuclei is assumed in
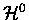 TC, the zeroth
order solution cannot distinguish the channel
TC, the zeroth
order solution cannot distinguish the channel  from
from  ,
into the
former of which the ground muonic state (
,
into the
former of which the ground muonic state ( )
should dissociate in
the limit
)
should dissociate in
the limit
 (recall the
(recall the  is more deeply bound
than the
is more deeply bound
than the  due to the reduced mass difference). The Improved
Adiabatic approach instead partitions the Hamiltonian into
due to the reduced mass difference). The Improved
Adiabatic approach instead partitions the Hamiltonian into
where the mass polarization (i.e. nuclear-muonic motion coupling)
term
 and the internuclear orientation term
and the internuclear orientation term
 ,
which were part of the perturbation
,
which were part of the perturbation
 in the
Adiabatic Representation, are now included in the zero order
Hamiltonian. The term
in the
Adiabatic Representation, are now included in the zero order
Hamiltonian. The term
 acting
in the nuclear centre of mass frame (as opposed to the geometric centre
of nuclei frame) breaks the symmetry, and causes the zero order muon wave
function to move to the heavier nuclei as
acting
in the nuclear centre of mass frame (as opposed to the geometric centre
of nuclei frame) breaks the symmetry, and causes the zero order muon wave
function to move to the heavier nuclei as
 [105]. Therefore, the Improved Adiabatic method is expected to
give more accurate results for the asymmetric nuclear case, compared to the
standard Adiabatic Representation approximation, for the same number of
basis functions N, hence achieving faster convergence. Of course, in the
limit
[105]. Therefore, the Improved Adiabatic method is expected to
give more accurate results for the asymmetric nuclear case, compared to the
standard Adiabatic Representation approximation, for the same number of
basis functions N, hence achieving faster convergence. Of course, in the
limit
 ,
both approaches should give the same results.
The two level approximation of the Improved Adiabatic method has been
applied by the Los Alamos group to the bound state calculations of
HD+ [105] and
,
both approaches should give the same results.
The two level approximation of the Improved Adiabatic method has been
applied by the Los Alamos group to the bound state calculations of
HD+ [105] and 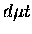 [57], as well as in the
scattering calculations [19,20,21]. The latter cover
all the possible combinations of muonic hydrogen isotope scattering,
including the only calculation to date of the hyperfine transitions in
asymmetric collisions.
[57], as well as in the
scattering calculations [19,20,21]. The latter cover
all the possible combinations of muonic hydrogen isotope scattering,
including the only calculation to date of the hyperfine transitions in
asymmetric collisions.
Despite the criticisms of the Adiabatic Representation, it should be noted
that the effective two level approximation used by Bubak and
Faifman (p. ![[*]](cross_ref_motif.gif) ) also deals with the dissociation
problem within the framework of the Adiabatic Representation, and appears
to give a reasonable accuracy for only N=2.
) also deals with the dissociation
problem within the framework of the Adiabatic Representation, and appears
to give a reasonable accuracy for only N=2.




Next: Variational approaches
Up: Adiabatic approaches
Previous: Multi-level calculations
![]() TC), and the perturbative term for the relative motions of the
nuclei as well as nuclear-muonic motion coupling (
TC), and the perturbative term for the relative motions of the
nuclei as well as nuclear-muonic motion coupling (
![]() ).
In the asymmetric nuclear system (e.g.,
Ma > Mb), since infinite
mass for both the nuclei is assumed in
).
In the asymmetric nuclear system (e.g.,
Ma > Mb), since infinite
mass for both the nuclei is assumed in
![]() TC, the zeroth
order solution cannot distinguish the channel
TC, the zeroth
order solution cannot distinguish the channel ![]() from
from ![]() ,
into the
former of which the ground muonic state (
,
into the
former of which the ground muonic state (![]() )
should dissociate in
the limit
)
should dissociate in
the limit
![]() (recall the
(recall the ![]() is more deeply bound
than the
is more deeply bound
than the ![]() due to the reduced mass difference). The Improved
Adiabatic approach instead partitions the Hamiltonian into
due to the reduced mass difference). The Improved
Adiabatic approach instead partitions the Hamiltonian into
![[*]](cross_ref_motif.gif) ) also deals with the dissociation
problem within the framework of the Adiabatic Representation, and appears
to give a reasonable accuracy for only N=2.
) also deals with the dissociation
problem within the framework of the Adiabatic Representation, and appears
to give a reasonable accuracy for only N=2.