


Next: Three body coulomb problem
Up: Muonic molecule and the
Previous: Muonic molecule and the
Accurate descriptions of muonic molecule
properties are essential to an understanding of 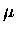 CF processes. The
energy levels of the loosely bound state
(J,v)=(1,1) affect the
temperature dependence of molecular formation rates; since 1 meV
CF processes. The
energy levels of the loosely bound state
(J,v)=(1,1) affect the
temperature dependence of molecular formation rates; since 1 meV  10
K, it is desirable to achieve an accuracy of better than 1 meV for the
energy level, which should be compared to the three body break up energy of
muonic molecular ions of
10
K, it is desirable to achieve an accuracy of better than 1 meV for the
energy level, which should be compared to the three body break up energy of
muonic molecular ions of  keV. In addition to the energy levels,
the molecular formation matrix elements are sensitive to details of the
keV. In addition to the energy levels,
the molecular formation matrix elements are sensitive to details of the
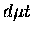 wave function, particularly in its asymptotic region, the
formation rates being proportional to the square of a wave function
parameter C (see Section 2.2). Furthermore, the
accuracy of the three-body wave function is important for
wave function, particularly in its asymptotic region, the
formation rates being proportional to the square of a wave function
parameter C (see Section 2.2). Furthermore, the
accuracy of the three-body wave function is important for
 sticking as well.
The convergence in variational calculations of the sticking probability
sticking as well.
The convergence in variational calculations of the sticking probability
 is much slower than that of the energy biding energy
is much slower than that of the energy biding energy
 ;
the general trend is that when
;
the general trend is that when  is converged to ncdigits,
is converged to ncdigits,  is accurate only to ns/3 significant
figures [3,84]. Thus, understanding two of the most
important processes in
is accurate only to ns/3 significant
figures [3,84]. Thus, understanding two of the most
important processes in 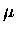 CF, i.e., molecular formation and
sticking, demands the solution of the three-body problem to an accuracy of
better than 10-7, a challenging task to the theorists. Indeed, in
1993, Szalewicz, one of the experts in the field, asserted these
calculations to be ``some of the most demanding few-body calculations,
taxing the most powerful supercomputers'' [85].
CF, i.e., molecular formation and
sticking, demands the solution of the three-body problem to an accuracy of
better than 10-7, a challenging task to the theorists. Indeed, in
1993, Szalewicz, one of the experts in the field, asserted these
calculations to be ``some of the most demanding few-body calculations,
taxing the most powerful supercomputers'' [85].
Because the three body problem is central to processes involved in this
thesis, we shall review its theoretical framework in some detail in the
sections that follow, focusing on understanding the underlying physical
concepts.



Next: Three body coulomb problem
Up: Muonic molecule and the
Previous: Muonic molecule and the